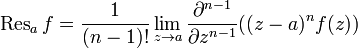Analyse complexe- théorème des résidus
21 messages
- Page 1 sur 2 - 1, 2
Analyse complexe- théorème des résidus
Bonjour à tous.
J'ai un problème pour appliquer le théorème des résidus lors du calcul d'une intégrale. L'intégrale en question est int(-R;R) (f(x) dx) avec f(x) = 1/(x^2+4)^4.
Les pôles sont donc 2i et -2i, on ne garde que 2i qui est dans le plan Im>0.
Comme c'est un pôle triple on applique
Res (f,2i)= 1/2 *lim x->2i (d^2/dx^2 ((x-2i)^3 *f(x))
soit Res (f,2i)= 1/2 *lim x->2i (d^2/dx^2 ((x-2i)^3 /(x^2+4)^3)
Or le calcul de la dérivée seconde est très long et pas très intéressant, ce n'est pas ce genre de calculs qu'on nous demande d'habitude.Je suis passée à côté de quelque chose pour éliminer le dénominateur ?
Merci de votre aide!
Cordialement
J'ai un problème pour appliquer le théorème des résidus lors du calcul d'une intégrale. L'intégrale en question est int(-R;R) (f(x) dx) avec f(x) = 1/(x^2+4)^4.
Les pôles sont donc 2i et -2i, on ne garde que 2i qui est dans le plan Im>0.
Comme c'est un pôle triple on applique
Res (f,2i)= 1/2 *lim x->2i (d^2/dx^2 ((x-2i)^3 *f(x))
soit Res (f,2i)= 1/2 *lim x->2i (d^2/dx^2 ((x-2i)^3 /(x^2+4)^3)
Or le calcul de la dérivée seconde est très long et pas très intéressant, ce n'est pas ce genre de calculs qu'on nous demande d'habitude.Je suis passée à côté de quelque chose pour éliminer le dénominateur ?
Merci de votre aide!
Cordialement
Salut,
Dans des cas comme celui là, perso, j'utilise... la définition : le résidu de f en 2i, c'est le coeff. en du développement en série de Laurent de
du développement en série de Laurent de ) :
:
=\frac{1}{\big((-4+4ih+h^2)+4\big)^4}=\frac{1}{(4ih)^4}\big(1+\frac{h}{4i}\big)^{-4})
Donc il te suffit de calculer le coeff. en du D.L. (classique) en 0 de
du D.L. (classique) en 0 de ^{-4}) et tu aura ta réponse.
et tu aura ta réponse.
Dans des cas comme celui là, perso, j'utilise... la définition : le résidu de f en 2i, c'est le coeff. en
Donc il te suffit de calculer le coeff. en
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
gizeh a écrit:Le problème est que ce n'est pas du (x^2+4)^4 mais du (x^2+4)^3 ! Donc pour appliquer son idée ça implique d'avoir x^2+4 au numérateur, ce qui complique la dérivée 3ème. On s'en sort mais c'est long aussi, en tout cas pas aussi simple que ce que Lionel a indiqué. enfin je crois?
Que vaut
gizeh a écrit:Est-ce que je continue à chercher dans cette voie ou est-ce que vous avez mal lu la question : je ne vois comment passer de mon énoncé :1/ (x^2+4)^3
à 1/(x^2+4)^4
sachant que si c'était j'arriverais à m'en sortir .
Je ne vois pas pourquoi tu dis que c'est un pôle triple, alors que c'est un pôle d'ordre 4.
A la limite, on peut faire comme ça... :ptdr:
Ben314 a écrit:Salut,
Dans des cas comme celui là, perso, j'utilise... la définition : le résidu de f en 2i, c'est le coeff. endu développement en série de Laurent de
:
Donc il te suffit de calculer le coeff. endu D.L. (classique) en 0 de
et tu aura ta réponse.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :