Analyse complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zwijndrecht
- Membre Naturel
- Messages: 85
- Enregistré le: 29 Oct 2020, 12:13
-
 par zwijndrecht » 19 Avr 2023, 15:31
par zwijndrecht » 19 Avr 2023, 15:31
Bonjour,
Soit

une fonction holomorphe sur le disque unité ouvert

.
On suppose que
|^{2n} \mathrm{d}\theta \leq 1)
, pour tout

et pour tout

.
Comment peut-on montrer que
| \leq 1)
, pour tout
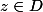
? Je ne vois vraiment pas par où commencer...
Merci d'avance pour votre aide !
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 19 Avr 2023, 16:31
par phyelec » 19 Avr 2023, 16:31
Bonjour,
votre fonction f est holomorphe sur D donc son module a un maximum M.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 19 Avr 2023, 19:11
par GaBuZoMeu » 19 Avr 2023, 19:11
Bonsoir,
Ça va nettement mieux si on dit "un maximum sur tout disque fermé de rayon
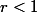
".
-
zwijndrecht
- Membre Naturel
- Messages: 85
- Enregistré le: 29 Oct 2020, 12:13
-
 par zwijndrecht » 20 Avr 2023, 09:07
par zwijndrecht » 20 Avr 2023, 09:07
J'y ai pensé, mais je n'obtiens pas grand chose...
Soit
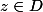
. On pose
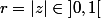
et
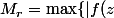| \; / \: |z| \leq r \} = \max\{ |f(z)| \; / \: |z| = r \})
.
On a, pour tout

,
|^{2n} \mathrm{d}\theta \leq M_r^{2n})
.
Ensuite, je ne vois pas trop comment faire pour en déduire que

...
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 20 Avr 2023, 12:33
par GaBuZoMeu » 20 Avr 2023, 12:33
Ce n'est bien sûr pas une majoration de l'intégrale qui va t'aider, mais une minoration.
Tu peux raisonner par l'absurde en supposant

; le but est alors de montrer qu'il existe un entier

tel que
|^{2n}\,d\theta >1)
.
-
zwijndrecht
- Membre Naturel
- Messages: 85
- Enregistré le: 29 Oct 2020, 12:13
-
 par zwijndrecht » 21 Avr 2023, 10:42
par zwijndrecht » 21 Avr 2023, 10:42
Ok, je tente quelque chose :
Supposons que

.
Il existe

tel que
| = M_r)
.
Par continuité de

, il existe
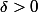
tel que
| \geq \left( \frac{M_r + 1}{2} \right) > 1)
, pour tout

.
Par suite,
|^{2n}\mathrm{d}{\theta} \geq \frac{1}{2 \pi}\int_{\theta_0 - \delta}^{\theta_0 + \delta} |f(re^{i \theta})|^{2n}\mathrm{d}{\theta} \geq \left( \frac{M_r + 1}{2} \right) ^{2n} \xrightarrow[n \to \infty]{} + \infty)
, ce qui est absurde.
Est-ce correct ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Avr 2023, 13:20
par GaBuZoMeu » 21 Avr 2023, 13:20
Presuqe.
Tu as vu l'idée, mais tu as juste oublié un petit facteur qui vient du fait que tu n'intègres pas sur
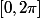
mais sur un intervalle de longueur
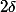
.
-
zwijndrecht
- Membre Naturel
- Messages: 85
- Enregistré le: 29 Oct 2020, 12:13
-
 par zwijndrecht » 21 Avr 2023, 13:24
par zwijndrecht » 21 Avr 2023, 13:24
Merci ! Effectivement...
Du coup, j'imagine qu'il suffit d'écrire ceci :
|^{2n}\mathrm{d}{\theta} \geq \frac{1}{2 \pi}\int_{\theta_0 - \delta}^{\theta_0 + \delta} |f(re^{i \theta})|^{2n}\mathrm{d}{\theta} \geq \frac{\delta}{\pi} \left( \frac{M_r + 1}{2} \right) ^{2n} \xrightarrow[n \to \infty]{} + \infty)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités