Analyse Complexe: Rotation

[Lostounet]

A mon sens, le seul passage non trivial, c'est f(D)=D et f(bord)=bord, mais c'est un simple calcul qui ne demande pas d'imagination.

Concernant f(bord) inclus dans bord, j'ai un peu de mal avec les calculs.

Si je note


Je me retrouve avec un truc du type: f(bord) =



J'ai dit qu'il était majoré par 1 puis je l'ai minoré par 1...
J'ai l'impression que c'est pas joli voire faux. Qu'en pensez-vous

[Ben314]

Tu es visiblement spécialiste du "pourquoi faire simple quand on peut faire compliqué" :

1) f est très clairement bijective de C\{un point} (ou éventuellement C tout entier) sur C\{un point} (ou éventuellement C tout entier) et la réciproque est immédiate à calculer -> on le fait et ça facilitera grandement les calculs d'images directe/réciproques de f.
2) L'inéquation |f(z)|<1 (resp. l'équation |f(z)|=1) équivaut à (resp. la même chose avec un =) qu'on sait parfaitement résoudre sans trop réfléchir (et dont il est de bon ton de connaitre les différents résultats possibles de ce type d'équation vu que ça intervient assez souvent soit en analyse complexe, soit en géométrie vu que les z->az+b sont des similitudes directes)

[Lostounet]

Prenons un instant pour remercier les programmes des lycées qui font qu'on arrive facilement en L3 sans trop savoir faire des calculs sur les complexes (ni trop sur quoi que ce soit d'ailleurs) et sans rien savoir sur les transformations de base du plan...

Je suis donc amené à calculer le module de:

qui vaut 1 parce que...

[Ben314]

Tu ne sait pas "développer" (a,b dans C) ?
Tu n'a jamais eu à résoudre en géométrie d'équation du style AM=2BM (A, B connus, on cherche les M) qui, en terme complexe, sont équivalentes à |z-a|=2|z-b| ?

[Lostounet]

Peut-être en considérant l'ensemble des points M du plan tels que M soit |u/v| fois plus loin de B que de A, d'affixes respectifs (u/v') et (v/u') avec les ' les conjugués... dans l'espoir que ce soit un cercle de centre 0 et de rayon 1.

[Ben314]

Pour résoudre par exemple AM=2BM, on l'écrit (où les carrés désignent les carrés scalaires) puis on peut soit "factoriser" : (où le point désigne le produit scalaire), soit, de façon un peu plus subtile, introduire un point G : qui, après développement, donne qui te dit explicitement que le truc malin, c'est de prendre pour G le barycentre de (A,1),(B-4).

Ca donne quoi en terme complexe ces raisonnement "bétassous" ?
Et c'est pas vraiment la peine de revenir en terme géométriques : a peu prés tout ce qu'on peut raconter en terme géométrique peut s'écrire directement en termes complexes (et plus ou moins vice-versa)

[Lostounet]

Bonjour,

Je dois retourner au collège...Désolé
Je vois pas trop comment faire sans une espèce de produit scalaire...
Supposons |z| = 1


=


Et à voir en quoi cos(?) = cos(?')...

A-t-on: ?



C'est pas joli

[Ben314]

Tu as pas l'impression que ça serait un tout petit peu plus pratique de partir comme ça :


Rappel :
Ce qui est très très exactement la même chose que :

[Lostounet]

Oui c'est vrai que c'est plus... lucide.
Merci Ben.

Je vais continuer ... On me demande de montrer ensuite que, pour tout w de D(0,1), il existe u et v tels que:
|u|^2 - |v|^1 = 1

J'ai dit, soit u et v tels que:




Ces u et v ont le mérite de vérifier la relation ...

Mais j'ai travaillé par implications donc je ne remonte pas vers f(z) identiquement nulle.

[Ben314]

On me demande de montrer ensuite que, pour tout w de D(0,1), il existe u et v tels que:
|u|^2 - |v|^1 = 1

Heuuuuu, c'est quoi l'intérêt du w ?
Tu n'aurais en plus la condition (i.e. f(0)=w) ou un truc du même style ?

[Lostounet]

Bonjour Ben

Oui bien entendu, il était tard.
Il me faut f(w) = 0 pour tout w c'est ce qui a motivé mon choix des modules

[Ben314]

Effectivement, si partant du système ( fixé tel que ) tout ce que tu obtient, c'est les valeur du module de et de , le moins qu'on puisse dire, c'est que tu as "procédé par implication", c'est à dire... que tu as allègrement jeté des équation à la poubelle en route...
Essaye de ne rien jeter à la poubelle et... ça se passera mieux...


P.S. : il y a évidement une infinité de solutions vu que, si est une solution et que est une rotation centré en 0 (i.e de la forme où ) alors la composée est clairement elle aussi une solution.

Il me faut f(w) = 0 pour tout w

J'ai un tout petit peu peur que ce soit pas trop cohérent avec le f(D)=D ton truc....

[Lostounet]

Bonsoir,

En fait j'avais résolu:




Afin de ne pas "jeter des informations précieuses", je me suis interrogé sur le sens de l'égalité de deux complexes: oui les modules sont égaux, mais mon raisonnement ne tient pas compte des arguments !

Fixons w dans D,




<=> (Si v nul, c'est toujours ok, si u nul c'est absurde, supposons ni u ni v nuls)





<=>





<=> ... ? Suis-je sur la bonne voie?

Il y a une autre question, encore pire, après avec des contraintes du type f(z0) = z1...

[Ben314]

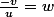
C'est peut être pas con de commencer par constater que ta première équation impose que donc en particulier que soit non nul (constatation que tu aurais du faire depuis longtemps vu que tu traine régulièrement des comme dénominateurs.

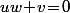
Ensuite, la deuxième équation si elle est sensée traduire que f(w)=0, ça serait nettement plus utile de l'écrire , c'est à dire (je te rappelle que tes inconnues, c'est u et v et que w est connu).
Donc cette équation te donne l'inconnue v en fonction de u et il n'y a plus qu'à reporter dans la première pour avoir le résultat :
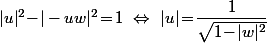
Il y a donc une infinité de solutions : on prend u quelconque ayant le bon module, puis .
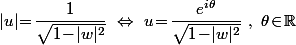
Si tu y tient vraiment (je suis pas sûr que ce soit utile), tu peut facilement paramétrer l'ensemble des solutions en écrivant que qui donne .

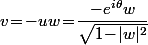
Et concernant la suite, il me semble qu'une fois que tu connais les fonctions telles que f(w)=0, c'est pas bien compliqué d'en déduire celles vérifiant f(z1)=z2 (je suppose que tu as montré précédemment que l'ensemble de ces fonctions formait un groupe)

[Lostounet]

Merci beaucoup Ben;

Pour le fait que ces trucs forment un groupe, j'ai montré que c'était un sous-groupe des automorphismes du disque (en utilisant la caractérisation f*g^-1 pour la loi "o").

Pour montrer que f(z1) = z2 la transitivité ... je ne m'y connais pas trop en "actions de groupes"...
Je peux donc, par le choix avéré de u et v, renvoyer n'importe quel élément de mon choix vers 0.

z1 --> 0 ---> z2

Je prends donc f et g de ce groupe en choisissant (u;v) et (u';v') tels que
f(z1) = 0
et g(z2) = 0

f(z1) = g(z2)
donc z1 = f^(-1) ( g(z2)) ... je sais pas

[Ben314]

Oui, c'est bien ça le principe, et il n'y a pas besoin d'être "grand druide" en action de groupe pour montrer que c'est équivalent au problème de départ :
On cherche toutes les fonction f telles que f(z1)=z2.
On fixe un fois pour toute une fonction g telle que g(z2)=0 (il en existe via la question précédente).
On a alors, pour toute fonction f, f(z1)=z2 <=> gof(z1)=0 : le sens => est trivial et le sens <= vient du fait que g est bijective.
Donc si H désigne l'ensemble des fonction h solutions de h(z1)=0, on a
f(z1)=z2 <=> gof=h est dans H <=> f=g^{-1}oh avec h dans H.

Remarque : on a pas besoin de considérer toutes les fonctions g telles que g(z2)=0 : une seule suffit, mais ensuite, il faut considérer toutes les fonctions h telles que h(z1)=0. On aurais évidement pu faire le contraire.

[Lostounet]

Merci Ben! J'ai compris.

Par contre a-t-on besoin d'expliciter u et v pour la fonction h (en fonction des u et v de la fonction f et de la fonctiong g, enfn trainer des racines de 1/(1-|z0|) )? Ou bien il suffit juste de montrer que f est dans le groupe et donc qu'ils existent?

Peut-on exprimer facilement en fonction des modules de z0 et z1 ou on s'en fout?
Le groupe c'est l'ensemble des fonctions de cette forme et tels qu'il existe u et v vérifiant |u|^2-|v|^2=1

[Ben314]

Par contre a-t-on besoin d'expliciter u et v pour la fonction h (en fonction des u et v de la fonction f et de la fonctiong g, enfn trainer des racines de 1/(1-|z0|) )? Ou bien il suffit juste de montrer que h est dans le groupe et donc qu'ils existent?
Peut-on exprimer facilement en fonction des modules de z0 et z1 ou on s'en fout?

Ca dépend comment la question est formulé :
- Montrer qu'il existe au moins une fonction f telle que ... <= Rien à expliciter, ni même donner l'ensemble des solutions.
- Déterminer l'ensemble des f telles que ... <= Pas clair s'il faut totalement expliciter les solution ou juste expliquer comment on les obtient (mais il les faut toutes)
- Déterminer explicitement l'ensemble des fonctions f telles que ... <= Là, oui, il faut "tout écrire" pour avoir du u=... et v=... (ou a la limite du u tel que |u|=... et v=...) en fonction de z1 et z2.

[Lostounet]

L'objectif étant de montrer que ce groupe est "transitif" et qu'il contient les rotations et que c'est donc l'ensemble de tous les automorphismes.
(de D)

Je vais essayer de faire des petits calculs pour expliciter u et v.
Pas sûr que ce soit très utile mais...faire des calculs me ferait du bien.