Algorythme d'Euclide

[MizaMiza]

Bonsoir,
Désolé du dérangement, mais j'aimerai avoir un coup de main concernant une question qu'il m'a été posée en cours ce matin: En utilisant l’algorithme d’Euclide, trouvez tous les entiers x ∈ Z tels
que le reste de la division de x par 6160 est ´egal au reste de la division de x par
12584. Je ne vois pas du tout comment m'y prendre afin de résoudre cet exercice, serait-il possible de m'expliquer comment y parvenir ? (J'aimerai avoir une démarche et/ou une explication, facilitant ainsi la compréhension)

[nodgim]

Savoir poser la bonne équation est déjà répondre à moitié au problème.
x = 6160 k + r = 12584 j + r
résous.

[MizaMiza]

Merci, mais du coup j'ai une équation à trois inconnue: x,j,k, je ne vois pas trop comment m'y prendre non-plus, pourrais-tu m'aider a dévelloper le résonnement ? Je sais que je suis un peu ennuyant xD mais c'est juste pour avoir une résolution pour pouvoir ensuite etre capable de résoudre tous les autres exercices du meme genre

[sylvainc22]

Je dirais que, pour commencer, n'importe quel entier entre 0 et 6159 fait l'affaire, ensuite on lui additionne n'importe quel multiple de ppcm(6160,12584) donc:

x = a + ppcm(6160,12584)

où 0 <= a <= 6159 et ppcm(6160,12584) = 6160*12584 / pgcd(6160,12584)

et bien sûr on a besoin de l'algorithme (pas y) d'Euclide pour le calcul du pgcd.

[MizaMiza]

Merci Bien! Je vous dirai quoi dès que j'ai le temps de vérifier tout cela. Mias il me semble que cette méthode ne donne pas toutes les valeurs possibles que x peut prendre, n'est-ce pas ?

[Kolis]

Bonsoir !
Mais non tu n'as pas trois inconnues : par différence,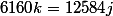 mais l'algorithme d'Euclide me semble ici sans aucune utilité !
C'est un théorème de Gauss qui est en cause.

[MizaMiza]

désolé mais je ne vois toujours pas comment m'y prendre pour trouver l'ensemble des solutions, quelqu'un pourrait-il résoudre l'exercice si possible ? Je suis sûr que la réponse est évidente mais je passe a coté

[nodgim]

L'algorithme d'Euclide permet de trouver le PGCD des 2 nombres, et donc le plus petit k tel que 6160*k = 12584*j.

[Pseuda]

Bonjour,

Reprends la démo de sylvainc22. x est solution ssi il existe r tel que 6160 et 12584 divisent tous deux x-r, ssi x-r est un multiple de 6160 et 12584 ssi c'est un multiple de leur PPCM.

Pour calculer leur PPCM, on peut utiliser le PGCD (=6160*12584)/PPCM), et pour calculer le PGCD on peut utiliser l'algorithme d'Euclide.

Mais peut-être tu ne sais pas le faire ?

[MizaMiza]

Bonjour,

Reprends la démo de sylvainc22. x est solution ssi il existe r tel que 6160 et 12584 divisent tous deux x-r, ssi x-r est un multiple de 6160 et 12584 ssi c'est un multiple de leur PPCM.

Pour calculer leur PPCM, on peut utiliser le PGCD (=6160*12584)/PPCM), et pour calculer le PGCD on peut utiliser l'algorithme d'Euclide.

Mais peut-être tu ne sais pas le faire ?

Malheureusement non, on vient de commencer la matière et j'aimerai bien comprendre comment résoudre ce type d'exercices car je n'en trouve aucun résolus dans mes manuels ou meme sur internet

[nodgim]

C'est tout de même bizarre qu'on demande dans ce problème d'utiliser l'algorithme d'Euclide alors que tu dis ne pas le connaitre.....

[MizaMiza]

C'est de l'avancement, je connais l’algorithme, je sais l'utiliser pour trouver des pgcd, mais je ne vois juste pas comment résoudre cet exercice. C'est pourquoi je demandais si quelqu'un savais le résoudre entièrement et peut être même m'expliquer les différentes étapes importantes pour trouver l'ensemble des solutions.

[Pseuda]

PGCD(6160,12584)=88 ; PPCM(6160,12584)=880880

Le reste de la division de x par 6160 est égal au reste de la division de x par 12584 ssi x=6160*q+r=12584*p+r avec 0<=r<6160 et 12584 soit 0<=r<min(6160,12584)
ssi x-r=6160*q=12584*p
ssi 6160 et 12584 divisent x-r
ssi x-r est un multiple de 6160 et de 12584
ssi x-r est un multiple de leur PPCM = 880880
ssi x=880880*k + r avec 0<=r<=6159

[MizaMiza]

AHHHH je viens de comprendre la possibilité de mettre un coeffiscient sur le ppcm
et que la variation était sur le resten, sincèrement dsl, merci beaucoup !!