Bonjour à tous
Je me permets d'ouvrir ce topic suite à une vidéo : https://www.youtube.com/watch?v=AgtOCNCejQ8
dans laquelle on nous donne la formule suivante pour trouver le minimum d'opération à réaliser afin de trier une liste (autour de 3min dans la vidéo) : N² / 2
Il est dit que si la liste contient 10 éléments alors le nombre d'opération N pour trouver le min = 10 , jusqu'ici aucun problème. On nous dit ensuite que pour trier cette liste (en trouvant le min -> extrayant et répétant) il faut alors 50 opérations , c'est ici que je loupe quelque chose.
Je pensais qu'on devait avoir N opérations = N+(N-1)+(N-2)+... , en retirant une opération à tous les tours (puisque je retire de ma liste un élément).
Quelqu'un pourrait m'expliquer le N ² / 2 svp.
Bonne journée.
Algorithmique : Tri d'une liste - Complexité
8 messages
- Page 1 sur 1
Re: Algorithmique : Tri d'une liste - Complexité
Bonjour Eclair Jaune,
reconnais-tu la nature de la suite dont tu as donné la formule de la somme des termes ?
Connais-tu une formule qui donne cette somme de termes ?
Le résultat n'est pas exactement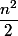 mais un équivalent.
mais un équivalent.
Cordialement,
reconnais-tu la nature de la suite dont tu as donné la formule de la somme des termes ?
Connais-tu une formule qui donne cette somme de termes ?
Le résultat n'est pas exactement
Cordialement,
Re: Algorithmique : Tri d'une liste - Complexité
La somme des n entiers (Gauss ) = n(n+1)/2 = 55 dans ce cas .
Re: Algorithmique : Tri d'une liste - Complexité
Je pense que dès le début, EclairJaune avait ce n(n+1)/2 en tête. Et donc 55, contre 50 dans la vidéo.
Et je pense que la question était pourquoi 50 plutôt que 55 ?
A mon avis, mais j'ai quand même des doutes, l'idée est de dire qu'on cherche un ordre de grandeur. Et quand n est grand, on ne garde que le terme de degré le plus élevé, et donc n(n+1)/2 est remplacé par n²/2.
Pour des calculs de complexité, et des estimations de temps de traitement, c'est complètement normal de faire cette approximation.
Ca me paraît un peu gênant de faire la même impasse, et d'annoncer un nombre 50 comme ça.
Environ 50 ou environ n²/2 ... ça aurait été très bien.
Et je pense que la question était pourquoi 50 plutôt que 55 ?
A mon avis, mais j'ai quand même des doutes, l'idée est de dire qu'on cherche un ordre de grandeur. Et quand n est grand, on ne garde que le terme de degré le plus élevé, et donc n(n+1)/2 est remplacé par n²/2.
Pour des calculs de complexité, et des estimations de temps de traitement, c'est complètement normal de faire cette approximation.
Ca me paraît un peu gênant de faire la même impasse, et d'annoncer un nombre 50 comme ça.
Environ 50 ou environ n²/2 ... ça aurait été très bien.
Re: Algorithmique : Tri d'une liste - Complexité
Exactement lyceen95 , en fait la vidéo est vraiment top et l'auteur arrive à vulgariser des sujets très techniques. Je me suis dit que ce ne pouvait pas être la somme des termes gaussienne qui était évoqué ici puisqu'il annonce 50 sans dire qu'il s'agit d'un ordre de grandeur ! Et du coup j'ai instantanément pensé à 55 et je ne comprenais pas l'écart.
Effectivement en faisant tendre vers + l'infini on pourrait résumer à n²/2 mais dans la vidéo les listes (10,100,1000) sont relativement petites.
Donc ce 50 devrait être 55 .
Effectivement en faisant tendre vers + l'infini on pourrait résumer à n²/2 mais dans la vidéo les listes (10,100,1000) sont relativement petites.
Donc ce 50 devrait être 55 .
Re: Algorithmique : Tri d'une liste - Complexité
Ou, plutôt que 50, "une cinquantaine".
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Algorithmique : Tri d'une liste - Complexité
Le tri proposé dans la vidéo s'appelle "tri par sélection", tu peux te documenter sur 
https://fr.wikipedia.org/wiki/Tri_par_s%C3%A9lection
https://fr.wikipedia.org/wiki/Tri_par_s%C3%A9lection
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
