Algorithme de la plus profonde descente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Als128
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Oct 2009, 12:43
-
 par Als128 » 07 Mar 2010, 21:36
par Als128 » 07 Mar 2010, 21:36
Bonsoir,
J'ai une question concernant mon cours d'optimisation.
Le cours en question définit le pas optimal de l'algorithme de descente du gradient (qui correspond à l'algorithme de la plus profonde descente)
Celui ci est définit ainsi : (J étant la fonction coût)
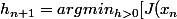-h\nabla J(x_n)])
Comment on fait pour additionner un scalaire avec un vecteur ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 07 Mar 2010, 23:02
par fatal_error » 07 Mar 2010, 23:02
salut,
)
est un vecteur non?
la vie est une fête

-
Als128
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Oct 2009, 12:43
-
 par Als128 » 07 Mar 2010, 23:37
par Als128 » 07 Mar 2010, 23:37
Ben justement, si la fonction cout est définie de R^2 -> R comment on fait pour ajouter J(x,y) à grad J(x,y) ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 08 Mar 2010, 00:01
par fatal_error » 08 Mar 2010, 00:01
ben chais pas, jconnais pas J...
Si tu dis que c'est une fonction de R^2 dans R, alors pe que le nabla n'est pas un laplacien mais un div.
M'enfin vu que c'est tas cité gradient jpenche quand même pour un laplacien...
En tout cas je peux pas plus t'aider.
M'enfin c'ets sur que additionne pas un scalaire et un vecteur...
Jpenche pour une virgule a la place du moins, ou alors J qui envoie pas dans R!
De mémoire, avec la méthode du gradient, on avait une jacobienne et une hessienne qu'on evaluait en certains points, mais jmarrete là avant de dire plus de conneries.
la vie est une fête


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Mar 2010, 00:11
par Ben314 » 08 Mar 2010, 00:11
Bon, je suis pas sûr d'y connaitre bien plus que fatal-error dans ces trucs d'optimisation, mais il me semble que le gradient de J, c'est la direction de plus forte pente (c'est donc un vecteur).
Si on en est au point xn, pour fair "baisser au max", il faut prendre cette direction, c'est à dire remplacer xn par xn+?.gradient.
Ca me fait me demander si c'est pas juste un problème de parenthèses ta formule, du style :
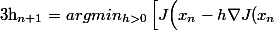\Big)\right])
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Als128
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Oct 2009, 12:43
-
 par Als128 » 08 Mar 2010, 08:43
par Als128 » 08 Mar 2010, 08:43
oui merci... je pense aussi que c'est une coquille.. je viens de voir ça avec la demonstration qui est explicitée plus loin...
-
Dihtbscii
- Membre Naturel
- Messages: 40
- Enregistré le: 07 Fév 2010, 18:23
-
 par Dihtbscii » 08 Mar 2010, 16:29
par Dihtbscii » 08 Mar 2010, 16:29
Oui c'est ça. Pour l'algorithme de la plus profonde descente on a la direction de descente et on cherche h qui minimise la fonction réelle f : R->R
x->J(xn+xd)
ou d est le gradient en xn ici.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
