Algèbre- Relation sur un ensemble

[Yozamu]

Bonjour à tous.

J'ai commencé cette leçon d'algèbre récemment, et je ne comprends pas du tout la leçon.
Particulièrement comment utiliser les définitions apprises, à savoir:

1) La relation est réflexive ssi:
Pour tout x appartenant à E, (xRx)

2) La relation est symétrique ssi:
(xRy)=>(yRx)

3) La relation est antisymétrique ssi:
[(xRy) et (yRx)]=>(y=x)

4) La relation est transitive ssi:
[(xRy) et (yRz)]=>(xRz)

Voilà ce que je pense avoir compris pour le moment(corrigez moi si je me trompe):
Relation d'equivalence cummule réfléxivité, symétrie et transitivité
Relation d'ordre c'est pareil mais antisymétrie à la place de symétrie.
Ensuite, (xRy) est équivalent à P(x,y) vraie (P etant une propriété).

Ensuite je suis moins sur de:
Reflexivité: si on a plusieurs variables on remplace par une unique x.. Enfin je sais pas trop comment expliquer donc je vais essayer avec des exemples pour voir si c'est cohérent:
Pour la relation x²-y²=x-y je dois prouver la reflexivité.
Je fais x²-x²=x-x donc xRx c'est bon ?
Autre exemple, (fRg)<=>il existe h bijective tq hof=goh
J'ai fait hof=foh et h bijective donc (fRf) donc réflexive?

Et puis pour les autres définitions, c'est le flou le plus total, pourriez vous essayer de m'expliquer, soit avec un cas général, soit en prenant les deux memes exemples que moi ?

Merci d'avance

[Scraaat]

Salut,

Les définitions sont en effet assez abstraites. Pour bien les comprendre, il est intéressant de les "sentir" sur les relations d'ordre et d'équivalence usuelles :

- Relation d'ordre : pense à la relation sur .
Elle est réflexive car
Elle est transitive car
Elle est antisymétrique car

- Relation d'ordre : la relation d'égalité sur .
Elle est réflexive car
Elle est transitive car
Elle est symétrique car


1) La réflexivité dit que tout élément est en relation avec lui-même, ie tu peux le "comparer" avec lui-même. Tes exemples sont bons, c'est bien compris.

4) La transitivité dit que la relation se "propage" : par exemple, la relation de divisibilité est transitive (c'est une relation d'ordre sur , tu peux t'entraîner à le montrer), car si divise et divise , alors divise .
Dans le cas de tes exemples : si tu as et , as-tu ?
S'il existe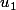 et 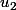inversibles tq et , existe-t-il un 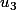inversible tq ?

La différence entre la symétrie et l'antisymétrie se visualise bien sur les deux exemples du début, je crois. Pour tes exemples :

2) Symétrie : , as-tu ?
, as-tu
Visuellement, tu dois pouvoir librement inverser les deux variables comme tu le veux.

3) Antisymétrie : si et , as-tu ?
S'il existe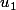 et 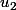inversibles tq et , as-tu ?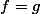


Voilà j'espère que c'est un peu plus clair, n'hésite pas à préciser tes questions :lol3:

Bon courage !

[Yozamu]

J'arrive vraiment pas à comprendre...

Voici ce que j'ai mis pour mes deux exemples, j'aimerais savoir ce qui ne va pas(autant au point de vue rédaction que réflexion...)

Le premier:
x²-y²=x-y
Reflexivité: x²-x²=x-x équivaut à 0=0 donc (xRx)
Symétrie: x²-y²=x-y
On multiplie par -1: y²-x²=y-x donc (yRx)
Transitivité: x²-y²=x-y et y²-z²=y-z
On additionne les deux équations et on obtient x²-z²=x-z donc (xRz)
Donc R est une relation d'équivalence

Le deuxieme:
Reflexivité: hof=foh car h est bijective; donc (fRf)
Symétrie: hof=goh et hog=foh car h bijective donc (gRf)
Transitivité: hof=goh et hog=ioh => hof=ioh car h bijective donc (fRi)
Donc R est une relation d'équivalence

[Scraaat]

Ça me paraît parfaitement compris du point de vue des définitions.


Par contre, je pense qu'il y a juste une petite incompréhension sur ta deuxième relation, peut-être dû à une confusion sur le "il existe h inversible..." :

I) Ainsi quand tu dis :

Reflexivité: hof=foh car h est bijective; donc (fRf)

ce n'est pas vrai.
Contre-exemple : et , alors mais , bien que f et h soient bijectives.
Cependant ta relation est bien réflexive : il faut montrer POUR TOUTE FONCTION , IL EXISTE une fonction inversible telle que : .
C'est pas très compliqué, il suffit de trouver h qui convient bien.

II) Ensuite,

Symétrie: hof=goh et hog=foh car h bijective donc (gRf)

est faux.
Déjà tu n'as pas forcément pour n'importe quelles fonctions (voir exemple au dessus), et si tu as alors tu as , ce qui n'est pas la même chose ! Tu as donc bien la réflexivité, mais la preuve n'est pas bonne car les fonction bijectives invoquées NE SONT PAS LES MÊMES. Proprement :
"Symétrie : pour tous x,y, si (xRy) alors (yRx)"
Ici il faut donc que tu montres (il te reste à trouver le bon h2) : "Pour toutes fonctions si ) alors

III) De même,

Transitivité: hof=goh et hog=ioh => hof=ioh car h bijective donc (fRi)

est faux.
En effet, il faut bien comprendre que comprendre que le raisonnement attendu est :
"Pour tout x,y,z, si ((xRy) et (yRz)) alors (xRz)"
On l'applique ici :
"Pour toutes fonctions si (() et ()) alors ()
C'est vrai, mais il faut le montrer proprement.


Deux derniers points, je te conseille de revoir les premiers cours de logique pour bien faire tes démonstrations : tu vois que pour la transitivité et la symétrie et l'antisymétrie, il s'agit d'une implication .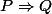
Il y a une seule bonne manière de démontrer clairement ça, et du même coup d'être sûr de son raisonnement : il faut supposer P est vraie, et montrer qu'alors Q est vraie.
Ex : Montrer la symétrie :
Soit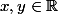 . SUPPOSONS QUE ( et ). ALORS , en ajoutant les égalités.

Dans le cas présent, pour la réflexivité par exemple, tu dois aussi montrer une proposition "pour tout x réel, ...".
Pour montrer cela, une seule possibilité : "SOIT x réel quelconque. ALORS ..."
Ex : Montrer la réflexivité : SOIT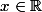 . ALORS donc (xRx).


Voilà dis-moi si tu comprends mieux ! :we:

[Yozamu]

Deux derniers points, je te conseille de revoir les premiers cours de logique pour bien faire tes démonstrations : tu vois que pour la transitivité et la symétrie et l'antisymétrie, il s'agit d'une implication .
Il y a une seule bonne manière de démontrer clairement ça, et du même coup d'être sûr de son raisonnement : il faut supposer P est vraie, et montrer qu'alors Q est vraie.
Ex : Montrer la symétrie :
Soit . SUPPOSONS QUE ( et ). ALORS , en ajoutant les égalités.

Dans le cas présent, pour la réflexivité par exemple, tu dois aussi montrer une proposition "pour tout x réel, ...".
Pour montrer cela, une seule possibilité : "SOIT x réel quelconque. ALORS ..."
Ex : Montrer la réflexivité : SOIT . ALORS donc (xRx).

Merci pour ce conseil j'essayerai de bien l'appliquer.
Donc il faut faire pareil pour l'antisymétrie et la transitivité?
Comme ceci je veux dire:
Antisymétrie: Supposons xRy et yRx Alors y=x (en remplaçant les relations par leur expression je veux dire, mais j'en avais pas sous la main..)
Transitivité: Supposons cRy et yRz Alors xRz
C'est ça ?

C'est pas très compliqué, il suffit de trouver h qui convient bien.

Je ne comprends pas trop surement a cause du concept de l'exercice.. "Trouver h qui convient bien", c'est à dire qu'en fait on doit prouver que la refléxivité est bonne quand h est égal à une fonction précise ? J'imagine que dire h=f n'est pas un bon résultat? Parce qu'autrement, je ne vois pas vraiment comment prouver cette refléxivité.. mais tu as mis hof=foh=f donc je vois pas trop comment ça peut être égal à f(D'ailleurs c'est pas marqué dans l'énoncé?). J'aurais tendance à penser alors que h=x... Bref les valeurs que je peux/dois prendre pour h sont pas claires pour moi

II) Ensuite,
Citation: Symétrie: hof=goh et hog=foh car h bijective donc (gRf)
est faux.
Déjà tu n'as pas forcément pour n'importe quelles fonctions (voir exemple au dessus), et si tu as alors tu as , ce qui n'est pas la même chose ! Tu as donc bien la réflexivité, mais la preuve n'est pas bonne car les fonction bijectives invoquées NE SONT PAS LES MÊMES. Proprement :
"Symétrie : pour tous x,y, si (xRy) alors (yRx)"
Ici il faut donc que tu montres (il te reste à trouver le bon h2) : "Pour toutes fonctions si ) alors

Je ne comprends pas pourquoi on peut(voire pourquoi on doit) avoir un h1 comme dans l'énoncé mais EN PLUS rajouter un h2? Sachant qu'en plus je ne connais la valeur d'aucune de ces deux fonctions, donc je ne vois pas comment raisonner
(De plus, je ne vois pas d'où sort la relation h1of=goh1 et h2of=hoh2 et en quoi elle prouve la symétrie)

III) De même,
Citation: Transitivité: hof=goh et hog=ioh => hof=ioh car h bijective donc (fRi)
est faux.

Je retrouve le meme problème ici: je n'ai aucune idée de comment choisir les valeurs de u1 u2 et u3, et donc je ne sais pas comment montrer "proprement"

[Scraaat]

Antisymétrie: Supposons xRy et yRx Alors y=x
Transitivité: Supposons cRy et yRz Alors xRz
C'est ça ?

Oui !

J'aurais tendance à penser alors que h=x...

C'est bien ça !!! Rédige la preuve proprement, et tu verras que ça prouve la réflexivité.

Je ne comprends pas pourquoi on peut(voire pourquoi on doit) avoir un h1 comme dans l'énoncé mais EN PLUS rajouter un h2?

Je pense avoir compris où ça coince : ta relation est défini par ")"
-> n'est pas fixée !!!
exemple : et . Alors en prenant
et . Alors en prenant
Ainsi, les fonctions utilisées ici sont différentes !

Récapitulons : pour prouver la symétrie, voilà le schéma de la preuve :
"Soient deux fonctions. Supposons que . Montrons que ."
Ici, ça se traduit ainsi : "Soient deux fonctions. Supposons que . Montrons que ." -> Tu CONNAIS , cette fonction est FIXÉE ; il te reste à TROUVER la bonne fonction pour que ça marche ! ( dépend de )

Je retrouve le meme problème ici: je n'ai aucune idée de comment choisir les valeurs de u1 u2 et u3, et donc je ne sais pas comment montrer "proprement"

Voilà le schéma :
"Soient des fonctions. Supposons que"
-> sont FIXÉES, tu ne les choisies pas !
Par contre, tu dois TROUVER telle que
Indice : commence par exprimer en fonction de et de , puis remplace par cette expression dans ta première relation (entre et


Voilà, tu vas voir qu'en manipulant tout ça, ça va devenir plus clair

[Yozamu]

En fait je pense que le probleme majeur vient précisément de cet exercice(même si je ne prétends pas avoir parfaitement compris le cas général).
En fait, je pensais que fRg <=> aof=goa
et que du coup gRf <=> aog=foa

Ce que je me dis, c'est que dans les relations, fRg ou gRf ou autre chose, la seule chose qui change dans n'importe quel cas, c'est ces fameux f et g, c'est pour ça qu'il me semble étrange d'avoir plusieurs h(h1, h2) ou encore des u(u1,u2,u3) alors que dans l'énoncé on a un simple h UNIQUE.

J'espere que le problème vient de ma compréhension de cet énoncé et non de la compréhension des définitions..

[Doraki]

Ton énoncé dit explicitement que
(fRg)il existe h bijective tq hof=goh

En fait, je pensais que fRg aof=goa

Pourquoi diable effaces-tu le "il existe .. tel que" de ta définition ? Tel que tu l'as écrit, ça ne veut plus rien dire parcequ'on ne sait pas si a est fixé quelquepart ailleurs dans la discussion, si on peut le choisir (ce qui est le cas) ou si c'est un truc qui doit être vrai pour tout a.

Je ne sais pas de quelle manière on peut reformuler le "il existe .. tel que" pour que ce soit clair, mais en aucun cas il faut l'enlever.
(fRg) tu peux trouver une fonction bijective h tel que h°f = g°h.
non (fRg) il n'existe aucune fonction bijective h tel que h°f = g°h

Parmi ces fonctions :
f1(x) = x+1
f2(x) = x+2
f3(x) = x²
f4(x) = |x|
f5(x) = x^3
f6(x) = x^5
peux-tu essayer de montrer que f1 R f2, f3 R f4, f5 R f6,
c'est à dire trouver dans chaque cas une fonction h (donc pas toujours la même) qui fasse l'affaire ?

[Yozamu]

Parmi ces fonctions :
f1(x) = x+1
f2(x) = x+2
f3(x) = x²
f4(x) = |x|
f5(x) = x^3
f6(x) = x^5
peux-tu essayer de montrer que f1 R f2, f3 R f4, f5 R f6,
c'est à dire trouver dans chaque cas une fonction h (donc pas toujours la même) qui fasse l'affaire ?

Je vois que je dois trouver un h différent pour chaque cas, mais je ne sais pas comment le choisir, parce que là déjà pour f1Rf2 je suis en train de tester plein de truc mais il doit y avoir une méthode dont je ne me souviens surement plus..

Mais donc pour la transitivité par exemple, on a deux "a" différent pour fRg et gRh, mais si les deux sont différents, j'arrive pas à montrer que fRh puisque visiblement rien ne lie fRg et gRh... Enfin c'est à vérifier après, mais vu que déjà j'arrive pas à déterminer la valeur des h que tu me demandes de trouver..

[Scraaat]

Je vois que je dois trouver un h différent pour chaque cas, mais je ne sais pas comment le choisir, parce que là déjà pour f1Rf2 je suis en train de tester plein de truc mais il doit y avoir une méthode dont je ne me souviens surement plus..

Tu VEUX avoir , c'est à dire .
Tu remplaces : tu VEUX avoir .
Peux-tu trouver une fonction qui convient ? (Fait un dessin pour t'aider)

Mais donc pour la transitivité par exemple, on a deux "a" différent pour fRg et gRh, mais si les deux sont différents, j'arrive pas à montrer que fRh puisque visiblement rien ne lie fRg et gRh... Enfin c'est à vérifier après, mais vu que déjà j'arrive pas à déterminer la valeur des h que tu me demandes de trouver..

Comme je le disais, tu AS et .
Comme est bijective, tu AS : , d'accord ?
Tu remplace g par ça dans ta première relation :
À partir ce cette égalité, vois-tu une fonction bijective telle que ?

[Doraki]

f1 R f2 est trouvable, mais oublie pour les autres (f3 R f4 est faux j'pensais à autre chose de moins restrictif et f5 R f6 c'est vrai c'est pas totalement trivial)

[Yozamu]

Pour f1Rf2, je dirais... h=2x?

Comme je le disais, tu AS et .
Comme est bijective, tu AS : , d'accord ?
Tu remplace g par ça dans ta première relation :
À partir ce cette égalité, vois-tu une fonction bijective telle que ?

Honnetement... Non.
On peut pas faire en sorte que les u2 "s'annulent" ? Parce que là y'aurait u=u1 mais je sais meme pas si je suis censé exprimer u en fonction de u1/u2 ou pas.

[Scraaat]

Pour f1Rf2, je dirais... h=2x?

C'est exactement ça :we:
Rédige la preuve pour t'en convaincre, et comme ça je pourrai te dire si ta rédaction est bonne.

Honnetement... Non.
On peut pas faire en sorte que les u2 "s'annulent" ? Parce que là y'aurait u=u1 mais je sais meme pas si je suis censé exprimer u en fonction de u1/u2 ou pas.

Tu as : . Qu'est-ce que tu obtiens si tu compose par des deux côtés de l'égalité ?

[Yozamu]

ho(x+1)=(x+2)oh
h(x+1)=h(x)+2
h(x+1)-h(x)=2
En fait j'ai pas de preuve... J'ai juste vu que avec 2x ça marche .. >_<

Qu'est-ce que tu obtiens si tu compose par u2 des deux côtés de l'égalité ?

U2oU1of=hoU2oU1
Donc u=U2oU1?

[Scraaat]

C'est tout bon.

Maintenant je te conseille :
1) de remontrer à cahier fermé que tes 2 exemples sont des relations d'équivalence, pour être bien sûr

Pour t'entraîner :
2) Montre que la relation définie par est une relation d'ordre sur
3) Montre que la relation définie par est une relation d'ordre sur
Est-ce que c'est une relation d'ordre sur ?
4) Soit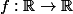 une fonction quelconque. Montre que la relation définie par est une relation d'ordre sur
5) Montre que la relation définie par est une relation d'ordre sur


Et reviens dès que tu as un doute =)

[Yozamu]

Mais pour h(x+1)-h(x)=2, ça suffit si je dit que h=2x convient...?

Merci pour l'aide et les conseils, je vais essayer de faire les exos d'entrainement!

[Doraki]

Ben tu dis "essayons de voir si h(x) = 2x convient :
h°f1(x) = h(f1(x)) = h(x+1) = 2x+2.
f2°h(x) = f2(h(x)) = f2(2x) = 2x+2.
Conclusion : h est une fonction bijective telle que h°f1 = f2°h, donc f1 R f2."

[Yozamu]

Ok, merci!