Bonjour à tous, je galère un peu à trouver la repose de cet exercice...
Soit f l’opérateur linéaire déini par :
f :R3[x]→R3[x]:p→p+p′ +p′′
Donner la matrice de f dans la base {1, x, x2, x3} , ainsi que son déterminant et son rang.
Merci pour votre aide !!
Algèbre première année bachelier
4 messages
- Page 1 sur 1
Re: Algèbre première année bachelier
Bjr
Il suffit de calculer l'image de chaque vecteur de la base canonique pour trouver la matrice de f:
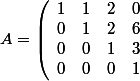)
Evidemment le déterminant vaut 1 et le rang est égal à 4.
Il suffit de calculer l'image de chaque vecteur de la base canonique pour trouver la matrice de f:
Evidemment le déterminant vaut 1 et le rang est égal à 4.
Re: Algèbre première année bachelier
aviateur a écrit:Bjr
Il suffit de calculer l'image de chaque vecteur de la base canonique pour trouver la matrice de f:
Evidemment le déterminant vaut 1 et le rang est égal à 4.
Peux-tu m'expliquer ça en détail stp ? Car j'ai du mal avec ce chapitre ....
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
