Voila je bloque dès le début sur mon dm ce qui fait que je ne peux pas avancer. Je ne sais vraiment pas comment m'y prendre si vous pouviez me donner des pistes ca m'aiderait beucoup!
Voici lénoncé: Soit F et G appartenant a C[X] de degre respectif m et n ac m=>n>0
Montrer sans utiliser la divison euclidienne qu'il existe un polynome T de degre N-1 au plus tq F(A)=T(A) pour toute racine A du poylnome G.
2/Montrer(sans calcul trop complexes) que si b= (1-racine(5))/2 ou b= (1=racine(5))/2 alors b^5 + b^3 +b+1=8b+5
Merci d'avance!
Algebre-Polynomes
7 messages
- Page 1 sur 1
J'ai fait plus que donner des indications. Ce polynôme est une banalité. Si tu as 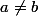 et c, d des réels, tu apprends au collège qu'il y a une seule fonction affine qui prend les valeurs c,d en a,b respectivement. Bon ben c'est pareil avec n valeurs données et un polynôme de degré au plus n-1.
et c, d des réels, tu apprends au collège qu'il y a une seule fonction affine qui prend les valeurs c,d en a,b respectivement. Bon ben c'est pareil avec n valeurs données et un polynôme de degré au plus n-1.
J'ai pas d'autre idée.
J'ai pas d'autre idée.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
