Algèbre polynôme de degré 3
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pitert
- Messages: 6
- Enregistré le: 04 Nov 2006, 15:39
-
 par pitert » 04 Nov 2006, 16:00
par pitert » 04 Nov 2006, 16:00
Bonjour,
Voila mon sujet:
Le but de cet exercice est de déterminer les racines d'un polynome arbitraire de degré 3. On considère donc l'équation suivante x^3+bx²+cx+d=0 (a,b,c et d sont des réels).
1) Grâce à un changement de variable adéquat, montrer que la résolution de l'équation ci-dessus se ramène à la résolution d'une équation du type x^3+px+q=0(E).
2) Soit x solution de l'équation (E) et soient u et v vérifiant x=u+v et 3uv+p=0,
montrer que u^3+v^3+q=0, en déduire les valeurs possibles pour u^3 et v^3 puis les racines de (E) (attention: les valeurs de u et v découlant de la connaissance de u^3 etv^3 ne vérifient pas toutes 3uv+p=0).
J'ai déja cherché la question 2 en effectuant un changement de variable dans l'équation mais je ne trouve pas 0.
En attente de vos réponse.
Merci
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Nov 2006, 16:34
par alben » 04 Nov 2006, 16:34
Tu as fait quel changement de variable et tu trouve quoi ?
-
pitert
- Messages: 6
- Enregistré le: 04 Nov 2006, 15:39
-
 par pitert » 04 Nov 2006, 16:46
par pitert » 04 Nov 2006, 16:46
j'ai posser u=x-v, v=x-u et q=-x^3-px=-(u+v)^3-p(u+v).
Jai remplacer dans mon équation et j'ai a la fin -3u²v-3uv²-pu-pv.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Nov 2006, 17:02
par alben » 04 Nov 2006, 17:02
met 3uv en facteur puis (u+v)
-
pitert
- Messages: 6
- Enregistré le: 04 Nov 2006, 15:39
-
 par pitert » 04 Nov 2006, 17:11
par pitert » 04 Nov 2006, 17:11
Merci pour ta réponse alben je trouve bien 0 à la fin maintenant.
Peut tu aussi m'aider pour la question 1 car sur celle là je bloque totalement.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Nov 2006, 17:18
par alben » 04 Nov 2006, 17:18
Pose x=t-b/3 et remplace
-
pitert
- Messages: 6
- Enregistré le: 04 Nov 2006, 15:39
-
 par pitert » 04 Nov 2006, 17:24
par pitert » 04 Nov 2006, 17:24
Qu'est ce que t??
Une nouvelle variable à introduire??
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Nov 2006, 17:32
par alben » 04 Nov 2006, 17:32
la question 1 te demande de faire un changement de variable, tu es donc bien obligé d'introduire une nouvelle variable et tu obtiendras une equation du type
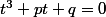
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Nov 2006, 17:42
par alben » 04 Nov 2006, 17:42
Tu as sans doute oublié un coefficient "a" dans la question 1, le changement de variable doit alors être x=t - b/(3a)
-
pitert
- Messages: 6
- Enregistré le: 04 Nov 2006, 15:39
-
 par pitert » 04 Nov 2006, 18:10
par pitert » 04 Nov 2006, 18:10
Alors voilà j'ai ca:
t^3-(t²b/a)+(tb²/3a²)-(b^3/27a^3)+t²-(2tb/3a)+(b²/9a²)+ct-(cb/3a)
Peut tu me dire si tu as ca, et comment simplifier.
merci
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Nov 2006, 18:25
par alben » 04 Nov 2006, 18:25
pitert a écrit:Alors voilà j'ai ca:
t^3-(t²b/a)+(tb²/3a²)-(b^3/27a^3)+t²-(2tb/3a)+(b²/9a²)+ct-(cb/3a)
Peut tu me dire si tu as ca, et comment simplifier.
merci
a[t^3-(t²b/a)+(tb²/3a²)-(b^3/27a^3)]+
b[t²-(2tb/3a)+(b²/9a²)]+ct-(cb/3a)+
dtu as oublié quelques coefficients
en les introduisant, les termes en t² doivent disparaitre
-
pitert
- Messages: 6
- Enregistré le: 04 Nov 2006, 15:39
-
 par pitert » 04 Nov 2006, 18:40
par pitert » 04 Nov 2006, 18:40
Voila après corection j'ai ca:
at^3-(tb²/3a)+(2b^3/27a²)+ct-(cb/3a)+d
Est ce que c'est bon?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Nov 2006, 19:08
par alben » 04 Nov 2006, 19:08
Oui c'est bon
Il te suffit de regrouper les termes par degré de t et de tout diviser par "a" pour obtenir quelque chose du genre attendu
t+\frac{d}{a}-\frac{cb}{3a^2}-\frac{b^3}{27a^3})
et d'identifier p et q :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
