La bijection, elle est surement pas entre les
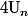
qui sont... des entiers, mais entre les

et autres
)
qui eux sont des ensembles.
Je vais te donner la réponse qui est... totalement évidente à condition de comprendre les notations de l'énoncé qui sont... très compliqués :
Lorsque tu as une suite du "fameux" ensemble
)
, c'est à dire une suite de 1 et de 2 dont la somme des termes fait n+3 et dont le dernier terme est un 1, si tu enlève le 1 de la fin, ça te fait une suite de 1 et de 2 dont la somme des termes fait n+2, c'est à dire un élément de
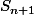
.
Réciproquement, si on part d'une suite de
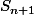
et qu'on lui rajoute un 1 à la fin, on obtient une suite de
)
ce qui signifie que la fonction
"ajouter un 1 à la fin de la suite" est une bijection de l'ensemble
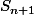
dans l'ensemble
)
Je te laisse deviner qui peut bien être la bijection de
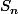
dans
)
...
Ensuite, comme tout élément de

et soit dans
)
, soit dans
)
, mais jamais dans les deux à la fois (because que, une suite de

, elle se termine soit par un 1, soit par un 2, mais pas les deux en même temps !!!) ça signifie que le cardinal
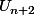
de

(i.e. son nombre d'éléments), c'est la somme du cardinal de
)
et de celui de
)
.
Mais grâce au bijections susmentionnées, on sait que
)
a autant d'éléments que
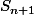
, c'est à dire

éléments et que que
)
a autant d'éléments que
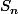
, c'est à dire
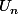
éléments.
Donc

Essaye de tout lire ce qu'il y a çi dessus jusqu'à ce que tu comprenne que c'est (plus ou moins) "bidon", c'est à dire que la "substantifique moëlle" du raisonnement, c'est juste de dire que, les somme de 1 et de 2 qui font n+2, sont
- Soit des sommes de 1 et de 2 qui font n+1 auxquelles on rajoute un "+1" à la fin
- Soit des sommes de 1 et de 2 qui font n auxquelles on rajoute un "+2" à la fin
