Algèbre linéaire

[Sourire_banane]

Salut,

En colle j'ai eu l'exo suivant :

Soit u un endomorphisme d'un espace vectoriel E de dimension finie. On considère sa restriction v à Im(u).
1) Comparer Tr(u) et Tr(v).
2) Si u est diagonalisable, v l'est-elle ?

J'ai traité que la première question (avec l'aide du prof) : Il faut chercher la forme des matrices de u et de v dans des bases adaptées et y lire qu'elles ont une même trace.
Maintenant si u est diagonalisable, je sais qu'une matrice de u dans une base donnée est semblable à une matrice diagonale qui comporte les vp de u sur sa diagonale, mais comme u et v ne sont pas définies dans les mêmes espaces et que les dimensions de ces espaces sont a priori différents, comment raisonner par matrices semblables ?
J'ai aussi pensé à une propriété sur la trace d'endomorphismes diagonalisables en rapport avec leurs valeurs propres, sauf que cela ne me donne aucune info sur la diagonalisabilité de v puisqu'on ne connait rien de u et de v, et donc sur leurs espaces propres.

Une astuce svp ?

[Ben314]

Salut,
C'est trés trés con : si dans la base la matrice de ton endomorphisme est diagonale alors il est clair que est le s.e.v. engendré par les correspondant à des valeur propres non nulles donc...

[Sourire_banane]

Salut et merci Ben314,

Je ne sais pas si j'ai très bien compris. Ce problème plutôt basique m'a déjà pas mal embrouillé sur des choses tout aussi basiques (th. de la base incomplète, comment traduire l'image d'un vecteur d'une certaine base dans la matrice de cet endo associé à cette base, etc.).
Alors en reprenant, dans ta base (f1, ..., fn) de l'espace E, on a u(fi)=lambdai*fi. Et à partir de cette base, on trouve les vecteurs qui s'écrivent u(...), donc ils appartient à Im(u) et on en crée une nouvelle base dans laquelle on pourra écrire v sous la forme de matrice diagonale ? Je t'avoue qu'en écrivant tout ça je n'ai pas bien saisi le but de la manoeuvre.

[Ben314]

(quasi) par définition, quelque soit la base de , est engendré par .
Si la matrice du est diagonale dans cette base alors et le s.e.v. engendré par tout les est évidement le même que celui engendré par les 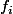tels que .
Ces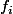 là forment une famille libre vu qu'ils sont extrait d'une base, donc ils forment une base de et dans cette base, la matrice de est diagonale.
En fait, la matrice de c'est donc celle de dans laquelle on a enlevé les lignes/colonnes colonnes où il y a un zéro dans la diagonale.

[Sourire_banane]

D'accord c'est déjà plus clair ;) Je vais digérer ton explication et revoir certains concepts qui devraient m'être évidents...

[L.A.]

Bonsoir.

Tu peux aussi utiliser un polynôme annulateur scindé à racines simples (si c'est à ton niveau), et généraliser ça à n'importe quelle restriction à un sev stable.