Algèbre linéaire

[lolo57]

Bonjour à tous,

Pour tout K-espace vectoriel E posons E*=L(E,K), et, pour toute base (e1,e2,...,en) de E, définissons e1*,e2*,...,en* appartenant à E* par:

ei*=(lambda 1 x e1+ ....+ lambda n x en)= lambda i

a)Montrer que (e1*,...,en*) est une base de E*, et que (e1**,...,en**) est une base de E**.

Soient f une application linéaire de E dans E* caractérisée par f(ei)=ei* pour tout i et g une application linéaire de E* dans E** caractérisée par g(ei*)=ei** pour tout i.

b)Montrer que f et g dépendent du choix de la base (e1,...,en) de E (Suggestion: étudier les cas E=K).

c)Montrer que h=gof l'application de E dans E** ne dépend pas du choix de la base (e1,...,en) de E (Suggestion: vérifier l'égalité (h(ei))(ej)*=ej*(ei)).

Voila l'exercice d'algèbre que j'ai à faire et je suis complétement bloqué. Si quelqu'un pouvait m'aider.

Merci d'avance.

[barbu23]

Bonjour, :happy3:

Pour ce qui est de la question n° : 1 :
Pour montrer que est une base de , tu fais comme suit :
Soit tels que : et tu montres que .
Ce que tu dois comprendre au passage, c'est que les ce sont des applications, et non des scalaires, comme c'est le cas de 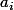. Une deuxième chose, c'est que dans ta recherche de la solution, tu dois utiliser le fais que . Le crochet de dualité joue le même rôle que le produit scalaire, c'est à dire, qu'il s'agit d'une application bilinéaire symétrique, et est le symbole de Kronecker que tu dois trouver dans ton cours et ce qu'il représente avec précision.
Cordialement. :happy3:

Edit : J'oublie une chose, il faut aussi, montrer que est une partie génératrice, pour cela, il faut montrer que s'écrit .

[hashintong]

Hello!

Quelqu'un saurait-il résoudre ces 2 algèbres linéaires?:




Ce serait un énorme plaisir de savoir l'explication!

Merci!!

[capitaine nuggets]

Bonjour à tous,

Pour tout K-espace vectoriel E posons E*=L(E,K), et, pour toute base (e1,e2,...,en) de E, définissons e1*,e2*,...,en* appartenant à E* par:

ei*=(lambda 1 x e1+ ....+ lambda n x en)= lambda i

@Barbu23 : J'ai du mal à comprendre la définition des .
Les scalaires dépendent-ils bien de i.e. dépendant de tels que ?

Une autre question.
Ne pourrais-t-on pas montrer que est libre et que pour prouver que est une base de ?

[Sourire_banane]

Hello!

Quelqu'un saurait-il résoudre ces 2 algèbres linéaires?:




Ce serait un énorme plaisir de savoir l'explication!

Merci!!

Salut,

Pour le premier je comprends pas.
Pour le deuxième, regarde si ta matrice est inversible (pivot de Gauss, toussa).

[LA solution]

Salut,

Pour le premier je comprends pas.
Pour le deuxième, regarde si ta matrice est inversible (pivot de Gauss, toussa).

pensee a utiliser le pivot Gauss