Algèbre linéaire, réduction ...

[Supernova]

Hey!

C'est encore moi avec une autre question cette fois-ci je souhaite mq où est un -ev de dimension 2, qui n'est pas une homothétie et est l'endomorphisme de qui à chaque associe l'endomorphisme .

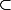
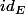
J'ai commencé par déterminer une base de qui est avec un vecteur non nul, ceci découle du fait que n'est pas une homothétie, on sait qu'on a cette inclusion mais pour l'autre ça revient à quoi faire? chercher la dimension de ou bien chercherà écrire les endomorphismes qui commutent avec en fonction de et ou c'est autre chose?

Merci !

[Supernova]

toujours pas d'idées??

[Supernova]

Tu peux utiliser l'argument de dimension. Ker(Phi_u) est dans E et dim E= .... Or ....

En fait phi_u est un endom de L(E)
dim(ker(phi_u)) = 3 ou 2 car sinon on aura ker(phi_u)=L(E) ce qui est faux car u n'est pas une homothétie mais comment écarter le cas où dim(ker(phi_u))=3
tu vois ...

[adrien69]

Tu peux utiliser l'argument de dimension. Ker(Phi_u) est dans E et dim E= .... Or ....

Nop raté ! Son est un opérateur sur un ensemble d'applications linéaires, pas sur E.

Je suis désolé j'ai la tête un peu prise Supernova, donc je n'arrive pas trop à me concentrer là-dessus, mais à ta place je chercherais deux applications linéaires non colinéaires dans l'image de , ça donnerait un truc bien pour le théorème du rang.

[Supernova]

Nop raté ! Son est un opérateur sur un ensemble d'applications linéaires, pas sur E.

Je suis désolé j'ai la tête un peu prise Supernova, donc je n'arrive pas trop à me concentrer là-dessus, mais à ta place je chercherais deux applications linéaires non colinéaires dans l'image de , ça donnerait un truc bien pour le théorème du rang.

oh non c pas grave Adrien mais ça fait une bonne indication, j’essaierai de l'exploiter, merci

[adrien69]

K c'est R, ou bien c'est C ?

[Supernova]

K c'est R, ou bien c'est C ?

c'est pas défini

[Supernova]

pourquoi tu le demande?

[adrien69]

J'ai la solution si K=C.

Dans le cas où u est diagonalisable, v commute avec u si et seulement si v est diagonalisable par la même matrice de passage, ça te laisse le choix sur les valeurs propres de v, il n'y en a que deux, donc tu as un espace de dimension 2.

Sinon, u est diagonalisable, soient m et n ses valeurs propres,
Si v est dans le noyau tu sais que v commute avec u si et seulement si v commute avec toute puissance de u.
Donc avec tout polynôme en u.
On se place dans la base de trigonalisation.

Si m=n on regarde (u-mId)v=v(u-mId)
sinon on regarde (u-mId)(u-nId)v=v(u-mId)(u-nId)

Dans les deux cas v doit commuter avec une matrice triangulaire supérieure stricte non nulle (si elle était nulle u serait diagonalisable car annulé par un polynôme scindé à racines simples)

On regarde en explicitant la matrice de v ce que ça nous donne sur les coefficients, et magique, ça nous donne un espace de dimension deux.


Par contre si K=R je ne sais pas, puisque je ne peux pas revenir d'une trigonalisation dans C à R.

[Supernova]

Sinon, u est diagonalisable

ici tu voulais dire que u est trigonalisable non?

[adrien69]

ici tu voulais dire que u est trigonalisable non?

Oui désolé. Regarde ce sur quoi je bosse, tu verras pourquoi je m'embrouille. C'est le fil de discussion sur la dominance stochastique.

[Supernova]

Oui désolé. Regarde ce sur quoi je bosse, tu verras pourquoi je m'embrouille. C'est le fil de discussion sur la dominance stochastique.

Ahhh !! bon courage, je sais que tu es capable de le démontrer (même si je n'ai rien compris)! ne reviens plus sur mon topic! concentre-toi sur le tien ^^
Bonne nuit!

[Supernova]

Hey! regardez ceci!

La famille (e, u(e)) constitue une base de E. Soit v dans L(E) qui commute avec u. On peut écrire v(e) = ae + bu(e)
Considérons alors w = aId + bu dans K[u]. v(e) = w(e) et
puisque v et w commutent avec u, on a aussi v(u(e)) = u(v(e)) = au(e) + bu^2(e)= w(u(e)). donc les v et w coincident sur une base, donc égaux!
ainsi v est dans K[u]. puis ker(phi_u)=vect(id,u)

[adrien69]

Hey! regardez ceci!

La famille (e, u(e)) constitue une base de E. Soit v dans L(E) qui commute avec u. On peut écrire v(e) = ae + bu(e)
Considérons alors w = aId + bu dans K[u]. v(e) = w(e) et
puisque v et w commutent avec u, on a aussi v(u(e)) = u(v(e)) = au(e) + bu^2(e)= w(u(e)). donc les v et w coincident sur une base, donc égaux!
ainsi v est dans K[u]. puis ker(phi_u)=vect(id,u)

Mouais, je préfère ma méthode :p

Elle est bourrin, incomplète, mais j'ai jamais su faire ce que tu viens de faire. :lol5:

[Supernova]

Mouais, je préfère ma méthode :p

Elle est bourrin, incomplète, mais j'ai jamais su faire ce que tu viens de faire. :lol5:

As you like