Algèbre linéaire polynome

[titi1]

bonjour, je n'arrive pas à démontrer que la famille constituée des vecteurs (a0,a1,...,aN) est une base de l'ensemble des polynomes de degré inférieur ou égal à N avec P(x)=a0+a1*x+...+aN*x^N.
Je vois juste qu'en dérivant N fois P on obtient 0 mais je ne vois pas trop comment répondre à cette question.
Merci d'avance pour votre aide

[jose_latino]

Une façon plus formelle de démonstrer que c'est une famille linéairement indépendante est la récurrence sur N et après tu peux faire la technique proposée pour toi.

[jose_latino]

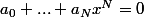
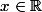
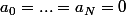
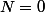
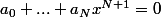
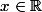
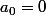
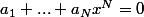
L'idée est demontrer que l'unique solution de (*), pour tout (mettre cette condition est très util) est , tu peux utiliser une récurrence: Si , c'est inmédiat, on suppose que (*) marche pour , si , pour tout (**), en particulier pour on a , en factorisant en (**), tu auras que , pour tout

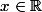
[fahr451]

bonjour

il y a confusion


si l'espace est RN[X]

(a0,...,aN) n 'est pas une famille de vecteurs mais une ligne de coordonnées

du seul vecteur P = a0+...+aN X^N

donc de quelle famille de polynômes parles tu ?

[jose_latino]

fahr451 a raison, j'ai considéré l'ensemble