Soit un problème du type
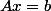
, avec :
)
Je souhaiterais comprendre les analogie avec la géométrie affine:
Puisque
=2)
, les solutions de ce système constitue un plan affine dirigé par :
=vect( \begin{pmatrix} 1 \\ -2 \\ 1 \\ 0 \end{pmatrix} , \begin{pmatrix} -1 \\ 1 \\ 0 \\ 1 \end{pmatrix}))
D'autre part puisque les deux premières colonnes de

sont libre (et engendrent

) tout élément de

(en l' occurrence
 s' exprime de manière unique dans cette base. Si l' on exprime cette solution en fonction des variables [tex]x,y)
(avec
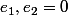
), on obtient:

, il s'agit là d'une solution particulière du système.
A priori les solutions du système précédent sont donc du type :
= \begin{pmatrix} 200 \\ 200 \\0\\ 0 \end{pmatrix} + vect( \begin{pmatrix} 1 \\ -2 \\ 1 \\ 0 \end{pmatrix} , \begin{pmatrix} -1 \\ 1 \\ 0 \\1 \end{pmatrix}))
La représentation des solutions de ce système n' est pas chose aisée puisqu'il faudrait que je me place dans un

de dimension 4 (
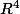
), cependant puisque nos variables

sont "liées" (je ne sais pas si cette terminologie qui est utilée pour caractérisé la dépendance linéaire de vecteurs peut l' être également pour des variables) c'est à dire qu'il existe une relation affine entre elles, je décide de me placer dans le plan
)
comme suit:
[attachment 23722 Capturer_graph.JPG]
D'autre part
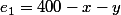
(relation affine): c'est donc l' écart par rapport à la droite affine d'équation
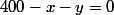
(Idem pour
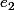
, qui représente l' écart avec la droite d'équation :
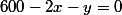
) on pourrait donc mesurer
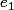
et
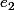
comme la distance/l' écart (via une échelle adaptée) par rapport aux droites affines définis précédemment (est ce que tout ceci est correcte ??).
Dès lors je souhaiterais représenter l' ensemble des solutions du système affine précédent (dans mon plan
)
si celà est possible).
On remarque que nos deux droites affines sont dirigées par les vecteurs

(resp.

) le ressemblance avec
)
est elle due au hasard ?
Ps: Aidez moi SVP j'ai mis deux heures à poster ce message mais je pense que vu comme je m' embrouille il en vaut la peine dans mon cas.
Sur le graphique on peut voir une solution évidente du système, il s' agit du point d'intersection des deux droites affines


