Algebre lineaire endomorphisme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 28 Oct 2011, 16:53
par elvis77 » 28 Oct 2011, 16:53
Bonjour à tous,
Voici mon souci :
on a un endomorphisme
)
et on suppose qu'

tel que
, u^{2}(x_{0}),...,u^{n}(x_{0})\})
est une famille libre où n est la dimension de E.
Montrer que u est un automorphisme de E.
Je n'arrive pas à exploiter l'hypothèse, j'ai essayé en me disant que toute sous-famille d'une famille libre est libre mais ça n'a rien donné.
Je ne sais pas comment trouver le
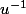
.
Si quelqu'un a une idée.
Merci
Cordialement
 par Exquise Sensation » 28 Oct 2011, 17:11
par Exquise Sensation » 28 Oct 2011, 17:11
elvis77 a écrit:Bonjour à tous,
Voici mon souci :
on a un endomorphisme
)
et on suppose qu'

tel que
, u^{2}(x_{0}),...,u^{n}(x_{0})\})
est une famille libre où n est la dimension de E.
Montrer que u est un automorphisme de E.
Je n'arrive pas à exploiter l'hypothèse, j'ai essayé en me disant que toute sous-famille d'une famille libre est libre mais ça n'a rien donné.
Je ne sais pas comment trouver le
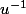
.
Si quelqu'un a une idée.
Merci
Cordialement
En algèbre on cherche rarement le
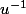
pour prouver la bijectivité.
Tu saurais comment prouver que u est surjective? C'est à dire que Im(u)=E sachant que Im(u)cE.
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 28 Oct 2011, 17:48
par elvis77 » 28 Oct 2011, 17:48
Merci pour votre réponse, elle m'a bien éclairée.
En effet, je me suis tout d'abord aperçu que finalement notre famille libre était une base de E (grâce à la dimension + le fait qu'elle est libre).
Pour montrer Im u = E, il suffit de montrer que
)
Soit
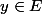
alors
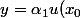+\alpha_{2} u^{2}(x_{0})+...+\alpha_{n} u^{n}(x_{0})))
et je cherche un x tel que
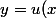)
il suffit d'écrire :
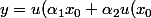+...+\alpha_{n}u^{n-1}(x_{0})))
donc x =
+...+\alpha_{n}u^{n-1}(x_{0}))
ok pour la surjectivité et pour l'injectivité je vais regarder ce ne doit pas être plus compliqué.
merci!
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 28 Oct 2011, 17:50
par elvis77 » 28 Oct 2011, 17:50
pour l'injectivité, il n'y a rien a dire puisque c'est une fonction linéaire elle, est forcément injective !
 par Exquise Sensation » 28 Oct 2011, 17:54
par Exquise Sensation » 28 Oct 2011, 17:54
elvis77 a écrit:pour l'injectivité, il n'y a rien a dire puisque c'est une fonction linéaire elle, est forcément injective !
Ui tu as la bonne idée sont que le résultat exact est:
Elle est linéaire ET les ensembles d'arrivée(E) et de départ(encore E) sont de même dimensions (car se sont les mêmes). donc surjective => injective
 par Exquise Sensation » 28 Oct 2011, 17:57
par Exquise Sensation » 28 Oct 2011, 17:57
elvis77 a écrit:Merci pour votre réponse, elle m'a bien éclairée.
En effet, je me suis tout d'abord aperçu que finalement notre famille libre était une base de E (grâce à la dimension + le fait qu'elle est libre).
Pour montrer Im u = E, il suffit de montrer que
)
Soit
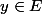
alors
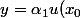+\alpha_{2} u^{2}(x_{0})+...+\alpha_{n} u^{n}(x_{0})))
et je cherche un x tel que
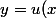)
il suffit d'écrire :
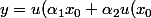+...+\alpha_{n}u^{n-1}(x_{0})))
donc x =
+...+\alpha_{n}u^{n-1}(x_{0}))
ok pour la surjectivité et pour l'injectivité je vais regarder ce ne doit pas être plus compliqué.
merci!
Ce que tu as fait est joli et juste rien à dire : ) En plus bête et méchant tu pouvais aussi affirmer que dim(Im(u))=n=dim(E) pour les raisons que tu as évoquées au début de ta preuve, et sachant que Im(u)cE cela te permet directement de conclure que Im(u)=E.
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 28 Oct 2011, 18:01
par elvis77 » 28 Oct 2011, 18:01
de mon côté je viens juste de montrer que Ker(u)=0 ce qui par le théorème du rang revient à dire que dim (Im u ) = n
merci de m'avoir aidé !
Cordialement, a bientot.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
