Bonjour,
je n'arrive pas à résoudre un exercice. Peut-etre pourriez vous m'aider ?
Soient n dans N*, (x1,..,xn) une famille de n vecteurs de E et (;)1,...,;)n) appartenant à R^n.
On a la famille (x1,...,xn+1) famille obtusangle de n+1 vecteurs de E.
Je dois montrer que la famille (x1,...,xn) est libre.
J'aimerais montrer que la relation est nulle et pouvoir en déduire le résultat mais je n'arrive pas à m'en sortir...
Merci
Algebre-famille obtusangle
4 messages
- Page 1 sur 1
Une idée peut-être ...
Obtusangle c'est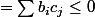 donc y=0
donc y=0
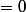 = sum de truc < 0 sauf si
= sum de truc < 0 sauf si  Pareil pour
Pareil pour 
Mmm ...
PS A ouais j'ai pas utilisé http://site.voila.fr/tpefu/Sans_titre.bmp
C'est sans-doute pas comme ça qu'il faut faire ...
Obtusangle c'est
Mmm ...
PS A ouais j'ai pas utilisé http://site.voila.fr/tpefu/Sans_titre.bmp
C'est sans-doute pas comme ça qu'il faut faire ...
C'est bien ca la définition de obtusangle, .
Supposons A strictement positif :
on a déduit que i;)j \geq0[/TEX] car
i;)j \geq0[/TEX] car  ;)i;)j
;)i;)j  0
0
donc y = 0, ce qui implique que ;)kxk = 0 => la famille de scalaire (;)k)k
;)kxk = 0 => la famille de scalaire (;)k)k [1..n] est nulle.
[1..n] est nulle.
or on a que i;)j < 0 , ce qui est impossible par hypothese d'ou A nul.
i;)j < 0 , ce qui est impossible par hypothese d'ou A nul.
Je sais pas si c'est possible. J'attends votre aide.
Supposons A strictement positif :
on a déduit que
donc y = 0, ce qui implique que
or on a que
Je sais pas si c'est possible. J'attends votre aide.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
