Algèbre Famille libre

[ArTiSTe]

Bonsoir,
je rencontre quelques problèmes sur une question que voici:
Soit f une application de R dans R telle que f(R) soit infini. Pour tout n de N*, posons f^n = f.f....f.
Montrer que S= (f^n)n pour n de N* est libre.
J'ai essayé pas mal de trucs mais je bloque. Je pense qu'il faut considérer une sous famille finie quelconque d'éléments de S et j'essaie de montrer qu'elle est libre en procédant par récurrence décroissante mais je bloque dès l'initialisation...
Merci d'avance pour votre aide!

[mathelot]

bonsoir,
comment est définie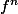 ? c'est un produit dans ou une composition ?
f est elle linéaire ?

[ArTiSTe]

Bonsoir,
C'est un produit dans R et f n'est pas forcément linéaire.

[SuperPoule]

Bonjour,

directement : soient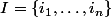 un sous ensemble fini et non vide de 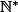et tels que : .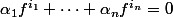
Pour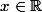 , en notant , on a alors : 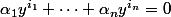. Or, prend une infinité de valeurs, donc que dire du polynôme ?

[ArTiSTe]

Je vois ... P a une infinité de racine donc c'est le polynôme nul, ce qui fait tomber tous les coefficients en même temps.
Merci beaucoup SuperPoule!
J'avais pas encore vu cette technique et ça a l'air assez puissant dans beaucoup de cas pour démontrer qu'une famille est libre. J'en prends note !