ah non pas du tout , j etais en train de le faire enfaite je trouve ceci :
a = 45/38
b= -27/95
c= -1/380
cette fois ci c est la bonne mdr
Algebre : Espace prehilbertion
32 messages
- Page 2 sur 2 - 1, 2
Re: Algebre : Espace prehilbertion
d(x,f) =  \left| \right|)
j espere que vous serrez d accord avec moi jusqu a la . Ensuite j aurais ca
 + 8 /9 x + 2/9 y +2/9 z
+ 8 /9 x + 2/9 y +2/9 z
2/9 x + + 1/18 y -1/18 z
+ 1/18 y -1/18 z
2/9 x -1/18 y + +1/18z
+1/18z
ou \varepsilon x)
17/9 x + 2/9 y + 2/9 z
2/9 x + 19/18 y - 1/18 z
2/9 x - 1/18 y + 19/18 z
a partir de la , je me suis bloque
j espere que vous serrez d accord avec moi jusqu a la . Ensuite j aurais ca
2/9 x +
2/9 x -1/18 y +
ou
17/9 x + 2/9 y + 2/9 z
2/9 x + 19/18 y - 1/18 z
2/9 x - 1/18 y + 19/18 z
a partir de la , je me suis bloque
Re: Algebre : Espace prehilbertion
oumou a écrit:cette fois ci c est la bonne mdr
Toujours pas, et à ta place ça ne me ferait pas trop rire de ne pas arriver à résoudre un tel système sans me tromper.
oumou a écrit:d(x,f) =
j espere que vous serrez d accord avec moi jusqu a la .
Non. Ce que tu écris après la première égalité ne veut strictement rien dire. Tu écris une différence entre un vecteur et une application linéaire.
Re: Algebre : Espace prehilbertion
c est bon , je renonce  euhh si non c est plutot P f (x) au lieu de P f pareil pour P f orthogonal , je viens de verifier dans mon cahier de cours
euhh si non c est plutot P f (x) au lieu de P f pareil pour P f orthogonal , je viens de verifier dans mon cahier de cours
 euhh si non c est plutot P f (x) au lieu de P f pareil pour P f orthogonal , je viens de verifier dans mon cahier de cours
euhh si non c est plutot P f (x) au lieu de P f pareil pour P f orthogonal , je viens de verifier dans mon cahier de coursRe: Algebre : Espace prehilbertion
Relire son cours est une bonne idée. Fais-le systématiquement (tout au long du cours, et pas seulement à 5 jours de l'examen).
Re: Algebre : Espace prehilbertion
loll...... si non on fait comment pour determiner le min ainsi que la sous question ?
Re: Algebre : Espace prehilbertion
Si tu as dans ton cours que \Vert) est la distance du vecteur
est la distance du vecteur  à
à  (sinon, tu le démontres comme je t'ai indiqué) et si tu as calculé le vecteur
(sinon, tu le démontres comme je t'ai indiqué) et si tu as calculé le vecteur ) , tu devrais être capable de calculer la norme de ce vecteur. Non ?
, tu devrais être capable de calculer la norme de ce vecteur. Non ?
(Au fait ce n'est pas une très bonne idée, si désigne un vecteur, d'appeler aussi
désigne un vecteur, d'appeler aussi  une de ses coordonnées).
une de ses coordonnées).
Pour la symétrie orthogonale, tu regardes dans ton cours comme on obtient la symétrie orthogonale par rapport à , et après le calcul de la norme vient tout seul. Commence au moins à écrire !
, et après le calcul de la norme vient tout seul. Commence au moins à écrire !
(Au fait ce n'est pas une très bonne idée, si
Pour la symétrie orthogonale, tu regardes dans ton cours comme on obtient la symétrie orthogonale par rapport à
Re: Algebre : Espace prehilbertion
quelle idiote !!!!  d(x,f) =
d(x,f) = 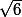
( \left| \right| = \sqrt{\sum_{}^{}{} x_{i} ^{2} + \sum_{}^{}{} y_{i}^{^{2}}+ \sum_{}^{}{}z_{i}^{2}}) )
)
la symetrie orthogonale ne figure pas dans notre cours mais je fais quelque chercher :
 [/tex]
[/tex]
 \left| \right|^{2} = \left| \right| x - y \left| \right|^{2} = \left| \right| x\left| \right| ^{2} + \left| \right| y \left| \right|^{2} -2< x, y > = \left| \right|x\left| \right|^{2} + \left| \right| P_{f}(x)\left| \right|^{2} + \left[ \right] 2x-P_{f}(x) \left| \right| ^{2})

 je sais plus
je sais plus
 d(x,f) =
d(x,f) = (
la symetrie orthogonale ne figure pas dans notre cours mais je fais quelque chercher :
Re: Algebre : Espace prehilbertion
Ca ne va plus du tout, là. ) serait indépendant de
serait indépendant de  ? Et que sont ces
? Et que sont ces  ,
,  et
et 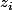 ?
?
Fais un "control reset" et essaie de repartir sur des bases plus saines.
On te demande de démontrer quelque chose sur "la symétrie de F" (sic) et tu n'as la définition de cette symétrie ni dans ton cours ni dans l'énoncé de l'exercice ? Je n'en crois rien. Peux-tu donner l'énoncé exact ?
Fais un "control reset" et essaie de repartir sur des bases plus saines.
On te demande de démontrer quelque chose sur "la symétrie de F" (sic) et tu n'as la définition de cette symétrie ni dans ton cours ni dans l'énoncé de l'exercice ? Je n'en crois rien. Peux-tu donner l'énoncé exact ?
Re: Algebre : Espace prehilbertion
alors je pense que d(x,f) = 
le voici :
on munit R3 de la sctructure euclidienne usuelle .on pose U1(1,2,2) U2 (1,3,1) U3 (0,1,2) on note P le projecteur orthigonal et S la symetrie orthogonale
1) montre que les vecteurs ( U1,U2,U3 ) forment une base de l espace vectoriel R3 .
2) En utilisant le procede de Gram-Schmidt , orthonormaliser la base ( U1,U2,U3) en une base ( e1,e2,e3) .
3) determiner la matrice de P dans la base (e1,e2,e3 )
4) determiner la matrice de S dans la base (e1,e2,e3 )
5) on note f = vect {u1,U2} et Pf +Pforthogonal =Id R3
a) determiner f orthogonal et donne une base orthinormale de f orthogonal
b) determiner d(x,f) = min
6) montre que \left|\right|^{2} = \left| \right|x\left| \right|^{2})
le voici :
on munit R3 de la sctructure euclidienne usuelle .on pose U1(1,2,2) U2 (1,3,1) U3 (0,1,2) on note P le projecteur orthigonal et S la symetrie orthogonale
1) montre que les vecteurs ( U1,U2,U3 ) forment une base de l espace vectoriel R3 .
2) En utilisant le procede de Gram-Schmidt , orthonormaliser la base ( U1,U2,U3) en une base ( e1,e2,e3) .
3) determiner la matrice de P dans la base (e1,e2,e3 )
4) determiner la matrice de S dans la base (e1,e2,e3 )
5) on note f = vect {u1,U2} et Pf +Pforthogonal =Id R3
a) determiner f orthogonal et donne une base orthinormale de f orthogonal
b) determiner d(x,f) = min
6) montre que
Modifié en dernier par oumou le 09 Mai 2016, 10:40, modifié 1 fois.
Re: Algebre : Espace prehilbertion
Ca ne peut pas être l'énoncé complet. Il y a trop de manques.
Je sors du fil.
Je sors du fil.
32 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
