Algèbre - Débutant...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Gyouji23
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Sep 2014, 22:03
-
 par Gyouji23 » 21 Sep 2014, 22:22
par Gyouji23 » 21 Sep 2014, 22:22
Bonjour,
Voilà je n'ai jamais vraiment fait d'algèbre linéaire auparavant, donc je suis débutant.
Je viens de passer des heures sur ma théorie, j'ai bien retenu la plupart des notions mais dès que je suis confronté à un exercice je suis perdu, je ne vois pas par où commencer.
Voilà l'exercice:
Dire si les ensembles suivants sont stables pour la multiplication (loi de composition):
A={n;)Z|;)k, l;)Z tels que n=k2;)l2}.
C={n;)Z|n=4k+1, k;)Z}.
(le "Z" est l'ensemble des entiers relatifs)
Est-ce que quelqu'un aurait la gentillesse de m'aider?
Merci vraiment beaucoup
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 21 Sep 2014, 22:27
par Bimbooo » 21 Sep 2014, 22:27
Il faut vérifier si A est stable par multiplication ? Et si C l'est ? Si c'est ça la question est : si je multiplie entre eux deux éléments de A, le résultat est-il dans A ?
Au fait k2 c'est k au carré ?

-
Gyouji23
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Sep 2014, 22:03
-
 par Gyouji23 » 21 Sep 2014, 22:35
par Gyouji23 » 21 Sep 2014, 22:35
Oui c'est ça, c'est bien la définition de "être stable" que je viens d'apprendre!
Et k2 c'est bien k au carré, désolé pour l'écriture...
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 21 Sep 2014, 22:58
par Bimbooo » 21 Sep 2014, 22:58
C'est pas grave

Alors si j'ai

dans

et

dans

par exemple, il existe l tel que
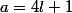
, et il existe

tel que
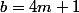
, alors soient de tels

et

.
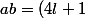(4m+1) = 4*(4lm) + 4l + 4m + 1 = 4(4lm + l + m) + 1)
.
On pose
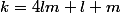
,

est bien un entier relatif,
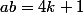
et
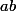
est bien dans

.

-
Gyouji23
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Sep 2014, 22:03
-
 par Gyouji23 » 21 Sep 2014, 22:59
par Gyouji23 » 21 Sep 2014, 22:59
En gros, mon problème, c'est de savoir quoi multiplier, comment le faire, et comment savoir si le résultat est dans A? Une petite aide serait vraiment la bienvenue.

-
Gyouji23
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Sep 2014, 22:03
-
 par Gyouji23 » 21 Sep 2014, 23:10
par Gyouji23 » 21 Sep 2014, 23:10
Merci beaucoup c'est super!!! Je te remercie vraiment!
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 21 Sep 2014, 23:13
par Bimbooo » 21 Sep 2014, 23:13
pas de souci, tu as tout compris ? Tu as fait l'autre ?

-
Gyouji23
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Sep 2014, 22:03
-
 par Gyouji23 » 21 Sep 2014, 23:22
par Gyouji23 » 21 Sep 2014, 23:22
Je bloque encore sur l'autre... mais je me pose une question: si on remplace 4k+1 par 4k+2 dans la donnée, on ne peut pas obtenir ab=4(4lm+l+m)+1, juste? Est-ce que A n'est pas stable dans ce cas là??
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 21 Sep 2014, 23:41
par Bimbooo » 21 Sep 2014, 23:41
Non ce n'est pas stable : si tu prends 6 = 4*1 + 2 et 2 = 4*0 + 2, 6*2 = 12 = 4*3 + 0 n'est pas dans l'ensemble

-
Gyouji23
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Sep 2014, 22:03
-
 par Gyouji23 » 21 Sep 2014, 23:46
par Gyouji23 » 21 Sep 2014, 23:46
Ok je commence à comprendre; le résultat doit absolument être sous la forme 4k+2 pour que l'ensemble soit stable...

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 22 Sep 2014, 05:35
par alm » 22 Sep 2014, 05:35
Pour le premier c'est stable:
Si
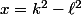
et
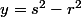
avec

alors le calcul direct donne:
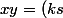^2+(\ell r)^2 - ((kr)^2+(\ell s)^2))
Une astuce consiste à remarquer que les double produit dans l'identité remarquable
^2=a^2+ 2ab +b^2)
est le même quand on developpe les carrés :
^2)
d'une part et
^2)
d'autre part.

-
Gyouji23
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Sep 2014, 22:03
-
 par Gyouji23 » 22 Sep 2014, 09:16
par Gyouji23 » 22 Sep 2014, 09:16
Salut, merci pour la réponse.
Je ne comprends pas; comment est-ce que tu passes de (ks)^2+(lr)^2 à (ks+lr)^2 ?
merci
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 22 Sep 2014, 13:01
par deltab » 22 Sep 2014, 13:01
Bonjour
Gyouji23 a écrit:Salut, merci pour la réponse.
Je ne comprends pas; comment est-ce que tu passes de (ks)^2+(lr)^2 à (ks+lr)^2 ?
merci
1) Quand tu as remplacé dans C, 4k+1 par 4k+2, tu as modifié l''ensemble C, le produit de 2 éléments de C doit rester dans C donc être de la forme 4k+2 et non 4k+1 (et c'est C et non A).
2) Pour la question que tu te poses maintenant, relis bien les indications données.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
