Algèbre commutative
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Em3
- Messages: 4
- Enregistré le: 23 Fév 2009, 11:27
-
 par Em3 » 23 Fév 2009, 11:34
par Em3 » 23 Fév 2009, 11:34
Bonjour,
J'ai un petit problème avec la démo d'un théorème,
Dans un anneau intégre A, on a
"(a) = (b)" (1) "équivalent à"
" il existe u élément inversible de A tel que a = u*b " (2)
(a) désigne l'idéal de A engendré par a
J'arrive à montrer que (2) entraine (1) mais pas la réciproque.
Merci pour tout aide.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 23 Fév 2009, 11:52
par ffpower » 23 Fév 2009, 11:52
Si a=0,alors b=0,donc on peut supposer a et b non nuls.Par def,(a)={au,u appartient a A}.Comme b est dans (a) il existe u tel que b=au.de meme,il existe v tel que a=bv.En multipliant les 2 égalités,on a ab=abuv.Par integrité de l anneau on a uv=1

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 23 Fév 2009, 11:53
par leon1789 » 23 Fév 2009, 11:53
)
donc il existe x tel que a=...
)
donc il existe y tel que b=...
Alors ab = ...
autrement dit ab(1-xy) = ...
Conclusion :
si ab=0 alors...
sinon...
EDIT : trop tard :triste:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 23 Fév 2009, 11:55
par leon1789 » 23 Fév 2009, 11:55
(2) implique (1) même si l'anneau n'est pas intègre.
[mode ThSQ]
Trouver un anneau commutatif non intègre tel que (1) n'implique pas (2)
[/mode]
-
Em3
- Messages: 4
- Enregistré le: 23 Fév 2009, 11:27
-
 par Em3 » 23 Fév 2009, 11:58
par Em3 » 23 Fév 2009, 11:58
Ah oui, il fallait JUSTE y penser ! :id:
Merci à vous 2 !
-
Em3
- Messages: 4
- Enregistré le: 23 Fév 2009, 11:27
-
 par Em3 » 23 Fév 2009, 12:02
par Em3 » 23 Fév 2009, 12:02
Oui j'avais remarqué que pour (2) => (1) l'intégrité n'était pas nécessaire.
Mais je ne vois pas de contre exemple... Je cherche...
-
Em3
- Messages: 4
- Enregistré le: 23 Fév 2009, 11:27
-
 par Em3 » 23 Fév 2009, 12:16
par Em3 » 23 Fév 2009, 12:16
Je ne trouve pas de contre ex...
Du type Z/kZ ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 23 Fév 2009, 12:18
par leon1789 » 23 Fév 2009, 12:18
Em3 a écrit:Je ne trouve pas de contre ex...
Du type Z/kZ ?
ça commence effectivement comme ça, mais il faut monter autre chose par dessus :id:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 23 Fév 2009, 16:33
par leon1789 » 23 Fév 2009, 16:33
A := Z[T] /
et t := classe de T dans A
Dans A, on a (2)=(2t) car
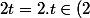)
et
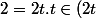)
.
Reste à voir que 2 et 2t ne sont pas multiples l'un l'autre par des inversibles !
Quels sont les inversibles de A ?
Montrer que 2 x (un inversible) = 2

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 23 Fév 2009, 16:55
par leon1789 » 23 Fév 2009, 16:55
A := Z[T] /
et t := classe de T dans A
Dans A, on a (2)=(2t) car
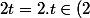)
et
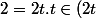)
.
Reste à voir que 2 et 2t ne sont pas multiples l'un l'autre par des inversibles !
Quels sont les inversibles de A ?
Montrer que 2 x (un inversible) = 2
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 23 Fév 2009, 19:32
par ThSQ » 23 Fév 2009, 19:32
leon1789 a écrit:(2) implique (1) même si l'anneau n'est pas intègre.
[mode ThSQ]
Trouver un anneau commutatif non intègre tel que (1) n'implique pas (2)
[/mode]
Intéressant (
euphémisme pour j'ai aucune idée 
).
Enfin le [mode ThSQ] en ce moment c'est je bourrine la phy et l'info !
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 23 Fév 2009, 22:16
par ThSQ » 23 Fév 2009, 22:16
Une suggestion pour le problème de Léon.
Idée : définir un anneau produit (sous-anneau de Z x Z/pZ[X], très peu d'éléments inversibles) avec un lien entre les deux coordonnées.
p premier > 3.
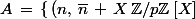, \, n \in \mathbb{Z} \, \})
. Edit : c'est pas super clair à le relire : ce sont tous les couples (n, (n mod p) + X*P(x))
A est un anneau non intègre et n'a que deux éléments inversibles.
On prend deux éléments non nuls et non opposés l'un de l'autre de Z/pZ : a et b.
Alors = mais (0, a*X) et (0, b*X) ne sont pas associés.
Léon, ton avis ?
-
SimonB
 par SimonB » 24 Fév 2009, 00:42
par SimonB » 24 Fév 2009, 00:42
ThSQ a écrit:Enfin le [mode ThSQ] en ce moment c'est je bourrine la phy et l'info !
Pas oublier le français... :ptdr:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Fév 2009, 08:51
par ThSQ » 24 Fév 2009, 08:51
J'ai lu le résumé de l'uvre, c'est bon ;)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Fév 2009, 20:19
par leon1789 » 28 Fév 2009, 20:19
ThSQ a écrit:Léon, ton avis ?
désolé pour le retard (-> petites vacances)
Ton exemple est assez amusant et intéressant. Je n'ai pas l'habitude de constructions dans ce genre (anneau = sous-anneau
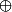
idéal), mais on en rencontre parfois. C'est une bonne idée de minimiser le nombre d'inversibles.
Sinon avec Z[T] / et t = classe de T
on a =
et l'ensemble des inversibles est 1+
donc 2 x (un inversible) = 2
et 2t x (un inversible) = 2t
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 28 Fév 2009, 21:48
par ThSQ » 28 Fév 2009, 21:48
leon1789 a écrit:minimiser le nombre d'inversibles.
Oui, c'est un peu de la triche

mais ça permet de simplifier le problème.
PS tout bronzé notre Léon ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Fév 2009, 22:11
par leon1789 » 28 Fév 2009, 22:11
ThSQ a écrit:PS tout bronzé notre Léon ?
tout, ou presque...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
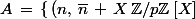, \, n \in \mathbb{Z} \, \}) . Edit : c'est pas super clair à le relire : ce sont tous les couples (n, (n mod p) + X*P(x))
. Edit : c'est pas super clair à le relire : ce sont tous les couples (n, (n mod p) + X*P(x)) 