Algèbre Bilinéaire

[sandrine_guillerme]

Bonjour tout le monde!

(ça fais un petit moment que chui pas venue y'en a qui n'ont en rien à cirer mais vous me manquez tous !!!!!!!)

Brefons ..
Je cherche une démonstration concrète du théorème suivant :

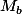
Soit la matrice de la forme bilinéaire symétrique dans la base B de E.
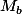
Alors l'application linéaire associée a aussi pour matrice pour la base B de E et la base duale B* de E* .

P.S: Si vous voulez tout savoir, je n'ai pas trop compris le rapport entre B et B* donc:
ma première question : B définit t elle B* ? si oui un petit exemple simple serait la bienvenue.
ma deuxième: Une petite démo svp ?


Merci :happy:

[jose_latino]

Salut Sandrine:
Le problème est que l'ennoncé est imcomplete et imprécis

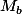
Soit la matrice de une forme bilinéaire symétrique dans une base B fixée de E.
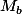
Alors l'application linéaire associée a aussi pour matrice pour la base B de E et la base duale B* de E* .

La définition de (il faut faire attention, cette application transforme un vecteur vers une fonction!!!!!) est:
définie par:

[sandrine_guillerme]

Salut José !

Tout ce que je peux dire c'est que je n'ai pas vraiment trop compris ..

[sandrine_guillerme]

(J'ai peut être trouvé une démonstration simple)

en utilisant le rang en fait :

et



Quelqu'un pour confirmer ?

[fahr451]

bonsoir sandrine qui parle comme édith cresson

j'ai cru comprendre que tu avais un problème avec la base duale
as tu compris la base duale ou non ?

[sandrine_guillerme]

Coucou fahr :p :p :p

ça fais un moment !!! (ça va?)

Ben a vrai dire un dual pour moi c'est l'espace vectoriel des formes linéaires (j'en vois ceux qui rient) mais c'est tout ce que j'ai compris ..

[fahr451]

j'ai toujours compris la même chose

je parlais de la base duale

[sandrine_guillerme]

Négatif,

à vous

[fahr451]

je ne comprends pas le morse pose une question j 'essaierai d y répondre

[sandrine_guillerme]

j'ai toujours compris la même chose

je parlais de la base duale

Non je ne comprends pas la base duale .. :triste:

[fahr451]

pour E de dim n

B = (e1,...,en) une base de E

on définit (f1,...,fn) la famille de formes linéaires par

f1(e1) = 1, f1(e2) = ...= f(en) = 0
etc fi(ej) = 1 si i = j 0 sinon

les f i sont parfaitement définies par les images des vecteurs de la base B

il reste à montrer que les fi forment une base de E *

je te laisse le faire ( je t'aiderai si tu as un problème)


on dit que (f1,...,fn) est la base duale de B notée B *

fi se note normalement ei *
on a donc ei *(ej) = 1 si i = j , 0 sinon

[sandrine_guillerme]

Code: Tout sélectionner

montrer que les fi forment une base de E *

Euh
elle est libre : immédiat.

Donc c'est une base
Non?

[sandrine_guillerme]

Je m'explique vu qu'on est en dim finie et que E et E* sont isomorphes quitte à montrer que la famille est libre (c'est quand même le plus simple!)





donc

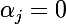
Et puis si vous êtes d'accord je veux bien une démo du théorème que j'ai énnoncé la haut SVP !

Merci

[fahr451]

pour la liberté d 'où vient

alpha 1 e1 +...+alpha n en = 0 ?

en fait

alpha 1 e1* +...alpha n en * = 0 implique en prennat l image de e1

alpha1 = 0 car e2* (e1) =...= en * (e1) = 0 et e1*(e1) = 1

etc

d'où la liberté.

ensuite sait-on que E et E* sont isomorphes? si oui c'est fini
si non on prend f une forme linéaire on pose f (ei) = alpha i

on considère la forme g = alpha 1 e 1 * +...+ alpha n en *

on a pour tout i g (e i) = alpha par définition des ej *
g et f coincident sur la base B donc sont égales et
les ej * forment une famille génératrice

[sandrine_guillerme]

Oui C'est bon là j'ai bien compris grace à toi !

Merci !