comment prouver que aleph 0 est le plus petit cardinal infini.
En effet j'ai un enoncé qui me demande de prouver dans un premier temps que c qui est le cardinal de R vérifie aleph 0<=c et aleph 0 différent de c.
Puis de démontrer que aleph 0 est le plus petit des cardinaux finis.
Merci d'avance.
Aleph 0
2 messages
- Page 1 sur 1
par legeniedesalpages » 12 Déc 2007, 01:49
Bonsoir,
Tu montres qu'il existe une injection de
dans 
En utilisant le théorème de Cantor, tu peux affirmer qu'il n'existe pas de surjection de sur )
,
ensuite montrer que est en bijection avec l'ensemble 
des suites de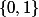 
, puis montrer qu'il existe une injection de dans 
(qui est en bijection avec )
grosso modo: = {0,1}^{\mathbb{N}} \preceq [0,1] = \mathbb{R})
prouver dans un premier temps que c qui est le cardinal de R vérifie aleph 0<=c
Tu montres qu'il existe une injection de
aleph 0 différent de c
En utilisant le théorème de Cantor, tu peux affirmer qu'il n'existe pas de surjection de
ensuite montrer que
grosso modo:
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :