Bonjour,
Je me présente, je suis étudiant en Licence, j'ai un exercice où je bloque totalement.
Les questions précédentes n'ont pas d'impact normalement pour cette question, le C trouvé est une expression somme totalement dégueulasse en fonction des a_i donc on va laisser pour l'instant le C.
C'est juste que je ne comprends pas ce qu'ils demandent..
En gros, il faut qu'on calcule l'aire de C(1 - alpha) < C < C(1 + alpha) ?
Donc je reprends l'aire de la question précédente et je soustrais la réunion de l'aire intérieure + l'aire de l'ellipse agrandi (ou rétréci selon alpha..) ?
Donc calculer l'aire de la "couronne" entre les deux ellipses modifiés ?
Mais comment calculer la réunion des aires ?
C'est là où je bloque, je ne sais pas quoi faire justement.. Une homothétie je l'interprete comme un "agrandissement" ou un "retrecissement" de l'ellipse..
Merci de bien vouloir m'expliquer ou me guider..
Aire et Homothétie d'une Ellipse
9 messages
- Page 1 sur 1
 Aire et Homothétie d'une Ellipse
Aire et Homothétie d'une Ellipse
Modifié en dernier par AquaSty le 23 Avr 2017, 00:23, modifié 2 fois.
Re: Aire et Homothétie d'une Ellipse
salut
si (u, v) est le centre de l'ellipse développe^2 + a(x - u)(y - v) + b(y - v)^2) ....
....
si (u, v) est le centre de l'ellipse développe
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Aire et Homothétie d'une Ellipse
Salut,
Merci pour ta réponse mais je n'ai pas compris ta réponse, désolé.. (sauf si tu parlais pour déterminer le centre ?)
le centre, je l'ai déjà trouvé avec le système des dérivées.
Là, l'équation (2) est déjà dans un repere de centre ( )
)
Mais je ne comprends juste pas comment calculer (la toute fin de la question)
(la toute fin de la question)
Merci pour ta réponse mais je n'ai pas compris ta réponse, désolé.. (sauf si tu parlais pour déterminer le centre ?)
le centre, je l'ai déjà trouvé avec le système des dérivées.
Là, l'équation (2) est déjà dans un repere de centre (
Mais je ne comprends juste pas comment calculer
Re: Aire et Homothétie d'une Ellipse
Salut, l'équation x² + y² = 4 dans un repère orthonormé définit le cercle de centre O et de rayon 2. Les points intérieurs au cercle sont définis par la condition x² +y²<4 et ceux à l'extérieur par x²+y²>4.
Cela fonctionne de la même manière pour les ellipses donc observe bien comment est défini ton ensemble et tu doit pouvoir facilement calculer ce qui est demandé à partir de l'aire de deux ellipses.
Cela fonctionne de la même manière pour les ellipses donc observe bien comment est défini ton ensemble et tu doit pouvoir facilement calculer ce qui est demandé à partir de l'aire de deux ellipses.
Modifié en dernier par jlb le 22 Avr 2017, 14:15, modifié 1 fois.
Re: Aire et Homothétie d'une Ellipse
Salut,
Merci pour ta réponse, mais donc si je comprends bien dans ta réponse avec le cercle, tu voulais plutôt dire x² +y²<-2 et x² +y²>2 ?
Car ici, c'est 2 homothéties avec) et
et )
Mais si j'essaye de raisonner en parallèle avec les cercles, donc ça revient à calculer :
} - \mathrm{A}_{ellipse(1 - \alpha)}) ?
?
Or} = \mathrm{A}_{ellipse(int)}*(1 + \alpha)^2) ?
?
Merci pour ta réponse, mais donc si je comprends bien dans ta réponse avec le cercle, tu voulais plutôt dire x² +y²<-2 et x² +y²>2 ?
Car ici, c'est 2 homothéties avec
Mais si j'essaye de raisonner en parallèle avec les cercles, donc ça revient à calculer :
Or
Re: Aire et Homothétie d'une Ellipse
Euh? oui pour le premier point et ensuite tu appliques la formule pour l'aire de ton ellipse avec C(1-alp) et ensuite C(1+alp) à la place de C!
( non, j'ai corrigé)
( non, j'ai corrigé)
Re: Aire et Homothétie d'une Ellipse
Ah d'accord, donc si j'ai bien compris (oui je peine un peu..) donc
} = 2\pi C(1-\alpha)(4a_2 - a_1^2)^{-1/2}) ?
?
(selon la question précédente où
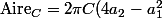^{-1/2}) )
)
Car je ne sais pas si le) doit être au carré ou pas (comme on est en présence d'une aire..)
doit être au carré ou pas (comme on est en présence d'une aire..)
(selon la question précédente où
Car je ne sais pas si le
Re: Aire et Homothétie d'une Ellipse
Pourquoi donc!! Tu utilises gentiment la formule en remplaçant C par C(1-alp).
Il te reste à recommencer pour C(1+alp) et ensuite calculer la différence entre les deux aires, différence correspondant à l'aire de la surface demandée.
[ l'aide te parlant d'homothétie, c'est pour te donner le lien entre la formule et ce que tu doit calculer ( c'est comme si tu multipliais l'équation initial par 1 + alp , dans le membre de droite tu fais apparaître le C(1+alp) et dans le membre de gauche les X'² et Y'² deviennent (racine(1+alp) X')² et (racine(1+alp)Y')² respectivement, d'où 'homothétie" en posant X" =racine(1+alp)X' et Y"=....
Il te reste à recommencer pour C(1+alp) et ensuite calculer la différence entre les deux aires, différence correspondant à l'aire de la surface demandée.
[ l'aide te parlant d'homothétie, c'est pour te donner le lien entre la formule et ce que tu doit calculer ( c'est comme si tu multipliais l'équation initial par 1 + alp , dans le membre de droite tu fais apparaître le C(1+alp) et dans le membre de gauche les X'² et Y'² deviennent (racine(1+alp) X')² et (racine(1+alp)Y')² respectivement, d'où 'homothétie" en posant X" =racine(1+alp)X' et Y"=....
Re: Aire et Homothétie d'une Ellipse
Ah ! C'est clair maintenant !
Merci jlb pour tes réponses ! Sympa ce petit forum, j'en ai fait plusieurs et à chaque fois on me repondait jamais alors qu'ici il y a une réelle réactivité, je reviendrai plus souvent
J'insistais avec le carré car j'avais lu ici :
http://dpernoux.free.fr/ExPE1/homothetie.pdf (Partie 2), propriété)
Si une figure F’ est l’image d’une figure F dans une homothétie de centre I et de rapport k et
si F a une aire égale à A alors F’ a une aire égale à k² × A.
Donc ça me mettait en doute..
Merci jlb pour tes réponses ! Sympa ce petit forum, j'en ai fait plusieurs et à chaque fois on me repondait jamais alors qu'ici il y a une réelle réactivité, je reviendrai plus souvent
J'insistais avec le carré car j'avais lu ici :
http://dpernoux.free.fr/ExPE1/homothetie.pdf (Partie 2), propriété)
Si une figure F’ est l’image d’une figure F dans une homothétie de centre I et de rapport k et
si F a une aire égale à A alors F’ a une aire égale à k² × A.
Donc ça me mettait en doute..
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
