Aire balayée par un arc avec déterminant

[Restefond34]

Bonjour,

Je suis en prépa MP en train de faire un exercice et le corrigé me semble étonnant. L'exerice souhaite prouver la loi des aires.
Il porte sur les arcs paramétrés : gamma est un arc, on cherche l'aire A(t) balayée : celle comprise entre le segment [0,gamma(0)], le segment [0,gamma(t)] et la courbe {gamma(s), s € [0,t]}.
Cependant, je ne comprends pas d'où sort cette formule de "Green-Riemann" qui est utilisée pour calculer l'aire.

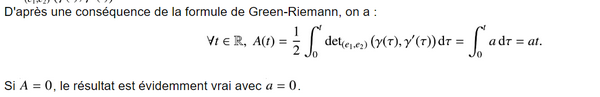
Je comprends "à peu près" la deuxième égalité (on utilise la formule d'un déterminant 2x2) et "il se trouve" que cela donne le produit vectoriel projeté. Mais la première faisant intervenir le déterminant me semble sortir de complètement nulle part.
Comment pourrait-on le justifier mathématiquement ?

Excellente soirée !

[Yezu]

Salut,

Avec les hypothèses nécessaires :
Soit de .
Green-Riemann te dit que si P et Q admettent des dérivées partielles continues sur un domaine D du plan délimité par un lacet fermé simple C, alors :


L'indication est la suivante : pour calculer l'aire d'un domaine D du plan, il suffit de trouver P et Q tel que : sur D.
On voit trivialement que et conviennent.
On a donc finalement :

[Restefond34]

Bonsoir,
Merci pour la réponse. Cependant, je ne suis pas sûr de vraiment tout saisir.
En vérité, cette formule faisant intervenir les intégrales sur un contour (comme en physique), nous ne l'avons pas vu en mathématiques et j'ai du mal à voir comment faire le lien avec l'aire.
Je me souviens vaguement que le déterminant est l'aire d'un parallélogramme, mais là, la surface considérée est plus complexe a priori...

[lionel52]

Une petite explication à la physicienne.
Ton origine de ton repère est O et tu veux calculer l'aire balayée quand tu te balades sur la courbe de à

Cette aire est égale à l'aire du triangle OMM' et pour rappel, dans le plan ça se calcule facilement avec un bon déterminant : (moitié de l'aire du parallélogramme porté par les vecteurs OM et OM')




Ou alors

[Yezu]

Salut,

Que ne saisis-tu pas dans mon indication ?

Le lien avec l'intégrale curviligne c'est Green-Riemann qui te le donne et je l'ai justifié dans mon indication.
L'idée c'est d'exploiter Green-Riemann pour transformer la formule classique du calcul d'aire dans le plan () en une intégrale curviligne.

[Restefond34]

Bonjour,

Merci pour vos réponses !

Pour lionel52, je comprends bien la démonstration "à la physicienne" mais est-elle parfaitement valable dans une copie ? En maths, nous ne sommes pas trop habitués au maniement du dt de cette façon... Je comprends qu'on se ramène à une surface infinitésimale mais est-ce bien légitime ?

Pou Yezu, en fait, je ne suis pas très à l'aise avec tout ce qui est intégrales doubles/curviligne (hors-programme en maths MP). Je pense avoir compris que l'aire était bien l'intégrale double de 1dxdy.
Ensuite, vous transformez cette intégrale en utilisant le théorème de Green-Riemann (en choisissant astucieusement P et Q). Mais c'est justement ce théorème de Green-Riemann (l'égalité aire -> contour) que je ne sais pas démontrer. Je ne sais pas si c'est plus clair ?

[Yezu]

Je comprends parfaitement tes inquiétudes, mais je ne comprends alors pas pourquoi dans ton corrigé il est mentionné "d'après une conséquence de la formule de Green-Riemann". Votre professeur vous a balançé la formule sans même expliquer ce qu'est une intégrale curviligne/intégrale double ? Si vous l'avez admise en cours, alors clairement je pense que tu n'as pas besoin de le démontrer dans une copie. Mais si tu préfères avoir la preuve pour ta propre curiosité, tu peux trouver plusieurs preuves sur un moteur de recherche (Green-Riemann ou Stokes au choix étant donné que le premier est un cas particulier du second).

[tournesol]

Ton prof a du aussi la jouer à la physicienne :

Arrivé à il a du écrire

[Restefond34]

Bonsoir,

Merci pour vos réponses !
Cet exercice ne vient pas de mon professeur, mais d'un recueil d'exercices d'oraux tombés aux ENS l'année dernière (RMS). Celui-ci est corrigé de cette façon et la formule semble être acquise (rien ne laisse supposer que la formule était donnée par l'examinateur)...
En cherchant des démonstrations sur Internet, j'ai l'impression de ne pas avoir le bagage suffisant pour la comprendre (intégrales multiples et contours avec des interversions). Je me contenterai de la démonstration physicienne, qui après tout est déjà pas mal, vu qu'on prouve la loi des aires !

[Yezu]

Salut,

Même si je ne suis pas spécialiste du programme français, je suis étonné que vous ne voyez pas les intégrales multiples et curvilignes en MP.
Et puis si le corrigé utilise la formule de Green-Riemann je ne vois comment elle ne serait pas étudiée en "MP". Elle était peut être donnée je ne sais pas.

[tournesol]

Les intégrales curvilignes et la formule de Green Riemann étant au programme de MP* , il est normal de l'utiliser pour corriger un exo psé à l'ENS .

[Restefond34]

Bonjour,

Malheureusement, je vous confirme que ça ne figure plus au programme et les 5/2 ont pu me le confirmer que ce n'était jamais vu en maths (le chapitre sur les arcs paramétrés est extrêmement court). Cela a disparu des nouveaux programmes (et l'exercice posé aurait du être conforme à ces nouveaux programmes)...
Ce document récapitule ce qui a disparu en page 2 : https://www.decitre.fr/media/pdf/feuill ... 413050.pdf

Donc j'imagine que la formule a du être proposée par l'examinateur finalement.

[Yezu]

Merci bien de vos confirmations Tournesol et Restefond34 !

[Aispor]

Salut Yezu ! Pourrais tu m'envoyer ton exercice ? Il m'intéresse beaucoup
Merci d'avance !

[Yezu]

Salut Aispor,

Malheureusement je ne suis pas le créateur de ce topic, je n'ai fait qu'aider Restefond34.
En espérant que ce dernier te communique l'exercice,

Bonne journée à vous

[Restefond34]

Bien sûr, pas de soucis, je l'ai !
Ce qui est fou je trouve, c'est que ça n'utilise aucune notion de dynamique (on ne définit pas vraiment de force, on se place juste implicitement dans le cas d'un mouvement à force centrale)

Le voici intégralement :

[Aispor]

Merci !