AIDEZ MOI POUR CALCULER CET LIMITE

par **abdelmalek.2008** » 03 Aoû 2018, 10:37

bonjour.
JE NE COMPRENDS PAS COMMENT CALCULER LA LIMITE:

par **hdci** » 03 Aoû 2018, 10:58

En écrivant

: quand x tend vers l'infini, c'est de la forme 1+X avec X->0

On peut alors faire un développement limité du logarithme :

Il n'y a plus qu'à développer.

par **abdelmalek.2008** » 03 Aoû 2018, 11:22

merci hdci.
pouvez vous m'expliquer plus en détail s-v-p.

par **hdci** » 03 Aoû 2018, 12:10

Connaissez-vous les développements limités ?

Le développement limité de

est

représente une fonction

où

(autrement dit,

est négligeable devant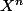

au voisinage de 0)

On utulise cette formule pour

en posant

: en effet quand x tend vers plus l'infini, X tend vers 0.

En notant f(x) la fonction dont on cherche la limite, on a donc

En remplaçant X par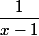

cela donne

On distribue le (x-1) :

Remarquons que

(appliquer la définition

...) il n'y a alors qu'à distribuer le x :

où

, une fonction de limite nulle quand x tend vers l'infini.

Le résultat est maintenant visible.

par **abdelmalek.2008** » 03 Aoû 2018, 14:05

merci beaucoup pour votre réponse