Aide démonstration - fonctions exponentielles et séries
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
maxnihilist
- Membre Relatif
- Messages: 166
- Enregistré le: 17 Fév 2013, 16:24
-
par maxnihilist » 27 Aoû 2013, 19:39
Bonsoir à tous,
Je suis devant une démonstration et je bloque au passage suivant :
(N pour la fonction de répartition de la loi normale)
Soit
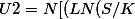) / (2 * sigma * sqrt(T) sqrt(p(1-p))) + (sqrt(n)*(p-1/2)) / sqrt(p(1-p)) ])
avec
 - e^(-sigma*sqrt(T/n)) ] / [e^(sigma*sqrt(T/n))-e^(-sigma*sqrt(T/n)) ])
Et je ne comprends pas l'affirmation :
En étendant les fonctions exponentielles dans une série, nous voyons que, lorsque n tend vers l'infini :
p (1 - p) tend vers 1/4
et
*(p-1/2))
tend vers
 sqrt ( T ) ] / 2*sigma)
PS : * pour multiplier.
PS2 : je sais que c'est moche sous ce format..
D'avance merci à tous
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
par deltab » 29 Aoû 2013, 00:27
Bonsoir
@maxnihilist
Il y peut-être des termes manquants où n'apparaissant pas à l'affichage (formule trop longue).
Je vais essayer de rendre tes formule plus lisibles
Soit
}{ 2 \sigma \sqrt{T} sqrt{p(1-p)} }<br /><br />+ \dfrac{sqrt{n}(p-\frac{1}{2})}{ \sqrt{p(1-p) }}\right))
avec
=.........????et
 \longrightarrow_{n \to \infty} \dfrac{ \left(r - \frac{\sigma^2}{2}\right) \sqrt{T} }{2\sigma})
Le '2' de U2 est-il une puissance, un indice ou fait partie de la notation.
Le 'LN' apparaissant dans U2 désigne-t-il bien le logarithme népérien (ln)?
Comme ça, tu pourra avoir de l'aide en espérant ne pas avoir modifies formules.
-
maxnihilist
- Membre Relatif
- Messages: 166
- Enregistré le: 17 Fév 2013, 16:24
-
par maxnihilist » 29 Aoû 2013, 12:36
Bonjour deltab,
le "2" de U2 fait bien partie de la notation. J'aurais pu dire tout simplement U, désolé.
La formule de U2 est bien correcte avec ta remise en forme, merci ! Concernant le membre du dessous, j'ai effectivement omis de préciser que c'était la valeur de p:
"Avec p = ... "
Le "ln" désigne bien le logarithme népérien.
Merci beaucoup pour tes notations.
En espérant que quelqu'un puisse m'aider sur ces points.
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
par deltab » 29 Aoû 2013, 16:12
Bonjour
@maxnihilist
En posant
, alors
, le problème se ramène à un calcul de de limite quand
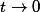
. Si une fonction F(t) admet une limite
quand
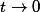
, alors la suite
)
converge vers la même limite
quand
.
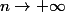
Si l'on pose
=\dfrac{ e^{rTt^2} - e^{-\sigma t \sqrt{T} }} {e^{\sigma t \sqrt{T}} - e^{-\sigma t \sqrt{T}}})
, alors
=p)
.
<br />=\lim_{t \to 0}\dfrac{2rTt e^{rTt^2} -\sigma \sqrt{T} e^{-\sigma t \sqrt{T} }} {\sigma \sqrt{T}e^{\sigma t \sqrt{T}} + \sigma \sqrt{T}e^{-\sigma t \sqrt{T}}}=\dfrac{1}{2})
(FI
, règle de l'Hôpital)
-\frac{1}{2}}{t})
est donc encore une FI
.On aura alors:
-\frac{1}{2}}{t}=\lim_{t \to 0}\dfrac{ 2e^{rTt^2} - e^{-\sigma t \sqrt{T} } - e^{\sigma t \sqrt{T}} } {2t(e^{\sigma t \sqrt{T}} - e^{-\sigma t \sqrt{T}})})
.
On ne vas pas utiliser le second membre pour le calcul de limite mais tenir compte du fait que
-\dfrac{1}{2})=\lim_{t \to 0}\dfrac{2rTt e^{rTt^2} -\sigma \sqrt{T} e^{-\sigma t \sqrt{T} }} {\sigma \sqrt{T}e^{\sigma t \sqrt{T}} + \sigma \sqrt{T}e^{-\sigma t \sqrt{T}}})
On aura alors
-\frac{1}{2}}{t}=\lim_{t \to 0}\dfrac{2rTt e^{rTt^2} -\sigma \sqrt{T} e^{-\sigma t \sqrt{T} }} {t(\sigma \sqrt{T}e^{\sigma t \sqrt{T}} + \sigma \sqrt{T}e^{-\sigma t \sqrt{T}})})
^2 e^{rTt^2} -\sigma^2T e^{-\sigma t \sqrt{T} }} {(\sigma \sqrt{T}e^{\sigma t \sqrt{T}} + \sigma \sqrt{T}e^{-\sigma t \sqrt{T}})+t(..)}=\dfrac{2rT - \sigma ^2 T}{2\sigma \sqrt{T}}=\dfrac{ \left(r - \frac{\sigma^2}{2}\right) \sqrt{T} }{\sigma})
???????????UP!!!! La méthode est bonne mais erreur de calcul quelque part, où?Calcul à revoir donc.
Pour la limite de p(p-1), calcules
(F(t)-1))
Remarque:"En étendant les fonctions exponentielles dans une série" revient à utiliser les DL de la fonction exponentielle qui sont les débuts du développement en série entière de la fonction exponentielle
-
maxnihilist
- Membre Relatif
- Messages: 166
- Enregistré le: 17 Fév 2013, 16:24
-
par maxnihilist » 30 Aoû 2013, 12:16
Bonjour
Merci pour ces éléments.
Concernant la limite pour p(p-1) il s'agit en fait de p ( 1 - p) et suivant cette méthode je retrouve les 1/4.
Je suis d'accord sur le raisonnement mais par contre je ne comprends pas ce passage (du moins le passage de la ligne précédente à cette ligne) :
^2 e^{rTt^2} -\sigma^2T e^{-\sigma t \sqrt{T} }} {(\sigma \sqrt{T}e^{\sigma t \sqrt{T}} + \sigma \sqrt{T}e^{-\sigma t \sqrt{T}})+t(..)})
et donc de ce fait ce passage aussi :
 \sqrt{T} }{\sigma})
???????????Pouvez-vous m'expliquer le principe ?
Merci
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
par deltab » 31 Aoû 2013, 00:10
maxnihilist a écrit:Bonjour
Merci pour ces éléments.
Concernant la limite pour p(p-1) il s'agit en fait de p ( 1 - p) et suivant cette méthode je retrouve les 1/4.
Je suis d'accord sur le raisonnement mais par contre je ne comprends pas ce passage (du moins le passage de la ligne précédente à cette ligne) :
Je suis arrivé à cette limite en utilisant la règle de l'Hôpital.
et donc de ce fait ce passage aussi :
???????????
J'ai juste écrit
}{2\sigma\sqrt{T}}= \dfrac{\sqrt{T}(2r - \sigma ^2)}{2\sigma}=\dfrac{2\sqrt{T}(r - \dfrac{\sigma ^2}{2})}{2\sigma}=\dfrac{ \left(r - \dfrac{\sigma^2}{2}\right) \sqrt{T} }{\sigma})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
