Affixe et CNS
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 29 Sep 2012, 08:47
par pantin » 29 Sep 2012, 08:47
Bonjour j'ai un exercice ou on me demande de:
(a,b et c sont les affixes)Je ne comprend pas que signifie la partie
Comme réponse, je propose :
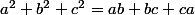
mais je ne suis pas sure.
Qu'en pensez vous ?
Merci
-
Anonyme
 par Anonyme » 29 Sep 2012, 08:56
par Anonyme » 29 Sep 2012, 08:56
une condition suffisante est si
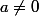
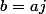
et

ou

et
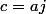
avec
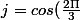 + i sin( \frac{ 2 \Pi }{ 3 }))
Remarque
On obtient la condition

mais je ne sais pas si c'est une CNS
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 29 Sep 2012, 08:59
par pantin » 29 Sep 2012, 08:59
je dois juste marquer ca donc ?
-
Anonyme
 par Anonyme » 29 Sep 2012, 09:05
par Anonyme » 29 Sep 2012, 09:05
pantin a écrit: Je ne comprend pas que signifie la partie "condition nécessaire et suffisante"
Tu te places dans le contexte de l'exercice : soit A(a) , B(b) et C(c) 3 points tels que ABC est un triangle équilatéral et tu recherches les conditions sur a,b et c
Puis tu pars de ces conditions et tu recherches si les 3 points A(a) , B(b) et C(c) forment un triangle équilatéral
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 29 Sep 2012, 09:08
par pantin » 29 Sep 2012, 09:08
Ah ok merci.
Mais une CNS c'est quoi en faite car c'est la première fois que je tombe sur celà ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Sep 2012, 09:09
par chan79 » 29 Sep 2012, 09:09
je dirais
c-a=
)
(b-a) ou c-a=
)
(b-a)
ce qui donne a²+b²+c²=ac+bc+ab
-
Anonyme
 par Anonyme » 29 Sep 2012, 09:11
par Anonyme » 29 Sep 2012, 09:11
pantin a écrit:je dois juste marquer ca donc ?
As toi de vérifier...
ExerciceSoit a, b et c sont 3 nombres complexes non nul et différents 2 à 2
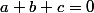
avec |a|=|b|=|c|
est-elle une CNS pour que A(a),B(b),C(c) forment un triangle équilatéral ?
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 29 Sep 2012, 09:14
par pantin » 29 Sep 2012, 09:14
a²+b²+c²-ab-bc-ca = (a+bj+cj²)(a+cj+bj²) ca irait ?
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 29 Sep 2012, 09:16
par pantin » 29 Sep 2012, 09:16
>ptinoir, je dirais que oui

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Sep 2012, 09:22
par chan79 » 29 Sep 2012, 09:22
je dirais
c-a=
)
(b-a) ou c-a=
)
(b-a)
ce qui donne a²+b²+c²=ac+bc+ab
-
Anonyme
 par Anonyme » 29 Sep 2012, 09:38
par Anonyme » 29 Sep 2012, 09:38
IL FAUT et IL SUFFIT d'analyser les 2 rotations de centre A(a) et d'angle dont une mesure est
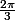
et
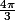
qui donnent ABC ou ACB comme triangle équilatéral
@chan79
As tu étudié tous ces cas ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Sep 2012, 09:57
par chan79 » 29 Sep 2012, 09:57
ptitnoir a écrit:IL FAUT et IL SUFFIT d'analyser les 2 rotations de centre A(a) et d'angle dont une mesure est
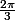
et
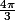
qui donnent ABC ou ACB comme triangle équilatéral
@chan79
As tu étudié tous ces cas ?
oui
c-a=
)
(b-a) ou c-a=
)
(b-a)
signifie
}-\fra{1}{2}).\fra{2}{\sqr{3}})
= i ou -i
Ecris que le carré est égal à -1
tu tritures tout ça et tu obtiens l'égalité
a²+b²+c²=ab+ac+bc
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 29 Sep 2012, 11:39
par pantin » 29 Sep 2012, 11:39
Je vous remercie tous de votre aide apporté , j'ai tout compris désormais.
Merci et bonne journée à tous :D
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
et
qui donnent ABC ou ACB comme triangle équilatéral