Affirmation à justifier

par **nico2b** » 07 Mai 2007, 10:10

Bonjour, voici l'énoncé que je dois justifier :

Soient a,b

Si

> 0, |a-b|

, alors a = b.

J'avais pensé à ceci :

Si on prend

avec n>0, on construira une suite positive tel que -

a-b

.

En passant à la limite, on obtient

d'où a = b.

Est-ce correct?
Merci

par **nico2b** » 07 Mai 2007, 10:19

Ah oui merci pour cette autre preuve
MErci

par **nico2b** » 07 Mai 2007, 18:39

RE-bonsoir, j'ai une autre affirmation à prouver là voici :

Si A est un sous-ensemble fermé de

et sup A

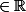
, alors sup A

A.

J'avais pensé à ceci :
A est fermé donc

.
Et par définition du suprémum, il existe une suite

.

Ensuite j'aurais pris dans l'hypothèse x = sup A et on a bien qu'il existe la suite qui converge vers ce x donc x

A...

Est-ce juste?
merci

par **fahr451** » 07 Mai 2007, 18:40

bonsoir oui

par **nico2b** » 07 Mai 2007, 18:54

merci beaucoup