L'adjoint d'un opérateur
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kammi
- Membre Naturel
- Messages: 63
- Enregistré le: 30 Nov 2011, 21:45
-
 par kammi » 05 Déc 2011, 21:17
par kammi » 05 Déc 2011, 21:17
salut,
svp, je doit montrer que dans un espace de Hilbert la norme d'un opérateur borné est superieur ou égale à celle de son adjoint.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 05 Déc 2011, 23:00
par girdav » 05 Déc 2011, 23:00
Bonjour,
tu te places dans le cadre des Banach ou des Hilbert ?
 par alavacommejetepousse » 05 Déc 2011, 23:22
par alavacommejetepousse » 05 Déc 2011, 23:22
bonsoir
ll f(x) ll^2 = < f(x) ,f(x) > = < x, f*(f(x)) > = < ll xll lll f* lll ll f(x) ll puis pour x tel que f(x) non nul
ll f(x) ll = < lll f* lll ll xll
ce qui prouve que lll f lll = < lll f * lll
ce qui est le contraire de ce que tu demandais mais en fait est également correct :we:
-
kammi
- Membre Naturel
- Messages: 63
- Enregistré le: 30 Nov 2011, 21:45
-
 par kammi » 06 Déc 2011, 05:14
par kammi » 06 Déc 2011, 05:14
girdav a écrit:Bonjour,
tu te places dans le cadre des Banach ou des Hilbert ?
je travaille dans un espace de Hilbert
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Déc 2011, 10:19
par girdav » 06 Déc 2011, 10:19
D'accord, donc dans ce cas
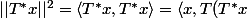\rangle\leq ||x||\cdot ||T||\cdot ||T^*x||)
puis on en déduit que

.
-
kammi
- Membre Naturel
- Messages: 63
- Enregistré le: 30 Nov 2011, 21:45
-
 par kammi » 07 Déc 2011, 07:42
par kammi » 07 Déc 2011, 07:42
girdav a écrit:D'accord, donc dans ce cas
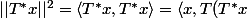\rangle\leq ||x||\cdot ||T||\cdot ||T^*x||)
puis on en déduit que

.
merci infiniment :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
