Bonjour,
"Justifiez que B(X, ε) ⊆ [B(X, ε)]"
N'est ce pas plutôt : B(X, ε) ⊆ [B_f(X, ε)] ?
N'importe quelle boule de rayon positif sur l'enveloppe de la boule ouverte contient des éléments de l'intersection avec celle-ci et fait donc partie de l'adhérence.
Adhérence d'une boule ouverte
9 messages
- Page 1 sur 1
Re: Adhérence d'une boule ouverte
B(X, ε) la boule ouverte centrée en X de rayon ε càd { X de R^p / norme de X < ε }
B_f(X, ε) la boule fermé càd { X de R^p / norme de X ≤ ε }
B_f(X, ε) la boule fermé càd { X de R^p / norme de X ≤ ε }
Re: Adhérence d'une boule ouverte
Tu ne réponds pas à ma question. Je te demande ce que désigne ton [B(X, ε)] (avec les crochets).
Re: Adhérence d'une boule ouverte
Ça me semble bizarre comme question. Pour moi la définition de l'adhérence d'une partie A d'un espace topologique X est "le plus petit fermé de X contenant A". Il est alors immédiat d'après la définition que toute partie est contenue dans son adhérence.
Mais peut-être t'a-t-on donné une autre définition de l'adhérence ? Laquelle ?
Mais peut-être t'a-t-on donné une autre définition de l'adhérence ? Laquelle ?
Re: Adhérence d'une boule ouverte
Adhérence de A : ensemble des X de 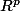 qui vérifient : ∀ℇ>0, A ∩ B(X, ℇ) ≠ ∅
qui vérifient : ∀ℇ>0, A ∩ B(X, ℇ) ≠ ∅
Re: Adhérence d'une boule ouverte
Il convient de montrer que tout élément de B(X, ℇ), ∀ℇ'>0, B(X, ℇ) ∩ B(X, ℇ') ≠ ∅ ce qui est trivial (il existe une distance non nulle entre l'élément et l'enveloppe de la boule).
L'adhérence d'une boule ouverte contient les éléments Y qui vérifient d(X - Y) = ℇ puisque pour tout ces Y il existe une suite de B(X, ε) qui converge vers Y.
Donc adhérence [B(X, ε)] = B_f(X, ε)
B(X, ε) ⊆ [B(X, ε)] est donc vraie puisque l'adhérence contient aussi l'enveloppe.
J'ai tout bon ? Je me suis embrouillé sur l'inclusion / inclusion stricte ..
L'adhérence d'une boule ouverte contient les éléments Y qui vérifient d(X - Y) = ℇ puisque pour tout ces Y il existe une suite de B(X, ε) qui converge vers Y.
Donc adhérence [B(X, ε)] = B_f(X, ε)
B(X, ε) ⊆ [B(X, ε)] est donc vraie puisque l'adhérence contient aussi l'enveloppe.
J'ai tout bon ? Je me suis embrouillé sur l'inclusion / inclusion stricte ..
Re: Adhérence d'une boule ouverte
Tu t'embrouilles complètement.
Posons=A) (ce qu'est
(ce qu'est  n'a en fait aucune importance).
n'a en fait aucune importance).
Il s'agit de montrer que pour tout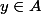 et tout
et tout 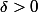 ,
, \cap A\neq \emptyset) .
.
Or il y a clairement un élément qui appartient à la fois à et à
et à ) . Tu vois lequel ?
. Tu vois lequel ?
Posons
Il s'agit de montrer que pour tout
Or il y a clairement un élément qui appartient à la fois à
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
