Adhérence / Intérieur d'une partie

[Supernova]

Bonjour!

Svp, à quoi faut-il penser à faire pour déterminer l'adhérence et l'intérieur d'un ensemble?


Merci

[zork]

par exemple si ton ensemble est fermé l'adhérence c'est lui-même
si l'ensemble est ouvert son intérieur c'est lui-même

sinon dans les autres cas il faut procéder par double inclusion en devinant d'abord quel pourrait être l'adhérence ou l'intérieur

[Supernova]

Il faut donc deviner..

[zork]

oui mais généralement c'est facile à deviner

[Supernova]

voilà mon ensemble: B={f £ C([0,1],IR): f(0)=f(1)=0} on voit que c'est un fermé, n'est-ce pas?

[zork]

je parlai pour l'adhérence et l'intérieur, en faisant un dessin, ca te donne une idée pour ces 2 choses

[Supernova]

dsl, j'ai pas bien compris ce que tu viens de dire

[cuati]

dsl, j'ai pas bien compris ce que tu viens de dire

En général cela dépend quand même beaucoup de la norme de ton e.v. (puisque c'est le cas d'un e.v. ici). Sans certitude, je ne connais pas ton niveau, j'imagine que B est muni de la norme du sup ?

[Supernova]

Zut! je suis tellement désolée de n'avoir pas indiqué que cet ev est muni de la norme infini.
Je suis en classe de maths spé

[cuati]

Zut! je suis tellement désolée de n'avoir pas indiqué que cet ev est muni de la norme infini.
Je suis en classe de maths spé

B est bien fermé.
Tu peux le voir, par exemple, comme l'intersection de deux images réciproques d'applications continue de dans ou alors à l'aide de suites de B...

[Supernova]

exactement !

Regarde, j'ai trouvé cette affirmation dans un topic mais j'ai pas compris d'où vient ceci:
<>

[cuati]

exactement !

Regarde, j'ai trouvé cette affirmation dans un topic mais j'ai pas compris d'où vient ceci:
>

Sous certaines conditions c'est possible mais ici je ne vois pas trop le rapport avec ton énoncé du début...

[cuati]

Oui, c'est vrai pour un sous-espace vectoriel. En effet, s'il n'est pas d'intérieur vide alors il contient une boule de rayon > 0. Or comme il s'agit d'un e.v. on peut par homothétie se ramener à une boule centrée en 0 et ensuite toujours du fait qu'il s'agisse d'un e.v. on peut dilater cette boule pour obtenir l'espace tout entier...ce que je viens d'écrire n'est pas une démonstration, c'est assez imagé... (tu peux faire la démo)

Pour ce qui est de ton exercice, tu peux aussi faire le lien suivant : considère comme un sous e.v. de .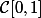
Soit alors essaye de construire une boule (pour la norme infinie) centrée en . Tu t'apercevras vite que cette boule ne reste pas incluse dans et que donc est d'intérieur vide, il n'est donc pas égal à 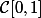tout entier... mais c'est pas vraiement une nouvelle...

[Supernova]

Oui, c'est vrai pour un sous-espace vectoriel. En effet, s'il n'est pas d'intérieur vide alors il contient une boule de rayon > 0. Or comme il s'agit d'un e.v. on peut par homothétie se ramener à une boule centrée en 0 et ensuite toujours du fait qu'il s'agisse d'un e.v. on peut dilater cette boule pour obtenir l'espace tout entier...ce que je viens d'écrire n'est pas une démonstration, c'est assez imagé... (tu peux faire la démo)

Pour ce qui est de ton exercice, tu peux aussi faire le lien suivant : considère comme un sous e.v. de .
Soit alors essaye de construire une boule (pour la norme infinie) centrée en . Tu t'apercevras vite que cette boule ne reste pas incluse dans et que donc est d'intérieur vide, il n'est donc pas égal à tout entier... mais c'est pas vraiement une nouvelle...

Ok, j'ai compris, merci pour ton aide

[cuati]

De rien, bonne continuation.

[Supernova]

De rien, bonne continuation.

C hyper gentil de ta part, bon continuation à toi également