Adherence d un connexe

[fou1234]

salut. svp comment montrer que l adhérence d un connexe est un connexe en utilisant le fait que ca n admet pas de séparation ( par contraposée)

[Ben314]

Salut,

comment montrer que l adhérence d un connexe est un connexe en utilisant le fait que ca n admet pas de séparation ( par contraposée)

Je comprend pas la question : je vois pas ce que désigne le "ça" (*) et je ne comprend pas non plus ce que vient faire une notion de "séparation" là dedans : ton espace topologique n'est pas forcément séparé ?

Je ne suis pas sûr non plus de comprendre le contexte : pour parler de convexe, je suppose qu'on se place dans un espace vectoriel (ou un espace affine ?) et pour parler d'adhérence, je suppose qu'on se place dans un espace topologique mais bien sûr il faut supposer un "lien" entre les deux structures si on veut espérer démontrer quoi que ce soit. En général, ce "lien", c'est qu'on suppose que les applications ainsi que sont continues. (c.f. Wikipedia par exemple)
C'est bien ça le contexte ?

(*) Je suppose qu'il y a une cédille et que ça se prononce "sa" et pas "ka".

[fou1234]

bonjour. j ai dit un ensemble connexe pas convexe. et pour separation je parle du fait qu un ensemble connexe n admet pas de separation. donc on supose que l adherence est non connexe (un ensemble qui admet une separation) pour montrer que l ensemble estnon connexe

[Ben314]

Mea culpa pour convexe/connexe.

Sauf que je vois toujours pas ce que tu peut bien appeler "une séparation".

Pour moi, la preuve "standard", c'est ça :

On se place dans un espace topologique et on considère une partie telle que, munie de la topologie restreinte, soit un espace topologique connexe.
On veut montrer que l'adhérence est aussi connexe (pour la topologie restreinte).

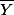Soit une partition de en deux ouverts de .
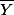Par définition de la topologie restreinte, on a et où et 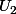sont deux ouverts de .
Donc et sont deux ouverts de qui forment évidement une partition de et, comme est supposé connexe, c'est que l'un des deux, par exemple est vide.
Sauf que ça signifie que, dans , le fermé contient donc il contient aussi son adhérence 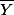ce qui prouve que est lui aussi vide.

SAUF QUE, ça peut éventuellement ne pas être ça la preuve que tu attend vu que celle là, c'est celle dans le contexte général des espaces topologiques alors que ton contexte à toi, ben je le connais pas vu que tu l'a pas donné...

[fou1234]

dans ma demonstration je ne sais pas comment demontrer que si O’∩Ā≠Ø alors O’∩A≠Ø