Bonjour,
J’ai un exercice à résoudre dont l’énoncé est :
Résoudre y’’(x)-y(x)=abs(tanh(x))
J’ai d’abord établi que la solution était de la forme a.exp(x)+b.exp(-x).
La méthode de variation des constantes m’a ensuite amené au résultat suivant :
a’(t)=abs(tanh(t))/(2.exp(t))
b’(t)=abs(tanh(t))/(-2.exp(-t))
J’ai vraiment du mal à intégrer ces deux fonctions. Aurais-je fait une erreur de calcul avant ? Ou alors aurais-je dû utiliser une autre méthode pour arriver à une expression différente de ce résultat? Ou alors existe t il une méthode pour intégrer ces fonctions ?
D’avance merci !
Y’’(x)-y(x)=abs(tanh(x))
6 messages
- Page 1 sur 1
Re: y’’(x)-y(x)=abs(tanh(x))
bonsoir,
tes égalités sont vraies.
pour les intégrer, on a, par exemple, pour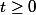
=\dfrac{tanh(t)}{2e^t}=\dfrac{e^t-e^{-t}}{2(e^t+e^{-t})e^t})
et on pose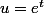 pour obtenir une fraction rationnelle de la variable u
pour obtenir une fraction rationnelle de la variable u
tes égalités sont vraies.
pour les intégrer, on a, par exemple, pour
et on pose
Re: y’’(x)-y(x)=abs(tanh(x))
tu dois trouver 2chx arctan e^x comme solution particulière , dont le signe est à adapter à cause de la valeur absolue . Pour moi , aucune solution n'est définie sur 
Re: y’’(x)-y(x)=abs(tanh(x))
Merci à tous les deux pour vos réponses.
Je tente ça ce soir et je reviendrai peut-être vers vous en cas de souci !
Je tente ça ce soir et je reviendrai peut-être vers vous en cas de souci !
Re: y’’(x)-y(x)=abs(tanh(x))
mathelot a écrit:bonsoir,
tes égalités sont vraies.
pour les intégrer, on a, par exemple, pour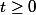
et on posepour obtenir une fraction rationnelle de la variable u
Re-bonjour,
C'est la méthode que j'ai choisi de suivre. J'ai ensuite décomposé ma fonction rationnelle de la variable u en somme de fonctions dont je peux déterminer une primitive et j'arrive donc à une expression de primitive pour cette fonction de la variable u.
Comment revenir ensuite à une expression de primitive pour a?
(Pour être tout à fait précis : j'ai une expression de G, primitive de g avec g une fonction rationnelle telle que
D'avance, merci.
Re: y’’(x)-y(x)=abs(tanh(x))
En fait je vais m'en sortir, c'est simplement qu'il faut faire intervenir la fonction arctan je crois 
Bonne journée.
Bonne journée.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
