50 résultats trouvés
Revenir à la recherche avancée
proba
Bonsoir, On lance une pièce de monnaie 3 fois. Soit X égale à 0 si on a pile au premier lancé ou X égale à 1 si on a face au premier lancé, et soit Y le nombre total où pile apparaît. 1) Trouver la loi de probabilité de X, Y, et (X,Y) \begin{tabular}{|l|M|P|} \hline X & 0 & 1 \\ \hline P(...
- 26 Nov 2019, 03:29
- Forum: ✯✎ Supérieur
- Sujet: proba
- Réponses: 1
- Vues: 185
Re: limite sup inf
5)On admet que \sum_{n=0}^{\infty}\mathbb{P}(A_n) < + \infty . Montrer que \sum_{n=0}^{\infty}1_{A_n} < + \infty presque surement. Ça parait simple mais je n'arrive pas à l'expliquer :( \sum_{n=0}^{\infty}1_{A_n}(x) = \lim_{n \rightarrow \infty} \sum_{p=0}^n 1_{A_p}(x) Le ca...
- 01 Nov 2019, 04:45
- Forum: ✯✎ Supérieur
- Sujet: limite sup inf
- Réponses: 3
- Vues: 387
Re: limite sup inf
Ok je vois c'est bon, la condition \mathbb{P}(C_0)< \infty est toujours vrai car c'est une mesure finie. C_n= \bigcup_{k \geq n} A_k alors (C_n)_n est une suite décroissante de \mathcal{A} et \mathbb{P}(C_0)< \infty donc \mathbb{P}(\bigcap_{n \in \mathbb{N}} B_n)= \li...
- 31 Oct 2019, 23:39
- Forum: ✯✎ Supérieur
- Sujet: limite sup inf
- Réponses: 3
- Vues: 387
limite sup inf
Bonsoir, On considère une espace probabilisé (\Omega , \mathcal{A}, \mathbb{P}) et une suite d'événements (A_n)_{n \geq 0} On définit également les ensembles suivants: \liminf_{n \rightarrow + \infty}{A_n}= \bigcup_{i \geq 0} \bigcap_{j \geq i}{A_j} ; \ \limsup_{n \rightarrow + \inft...
- 31 Oct 2019, 03:02
- Forum: ✯✎ Supérieur
- Sujet: limite sup inf
- Réponses: 3
- Vues: 387
Re: Proba
je ne vois pas 

- 22 Juin 2017, 01:17
- Forum: ✯✎ Supérieur
- Sujet: Proba
- Réponses: 7
- Vues: 322
Re: Proba
Y= 1 si X est entre 0 et P sinon 0.
- 21 Juin 2017, 19:07
- Forum: ✯✎ Supérieur
- Sujet: Proba
- Réponses: 7
- Vues: 322
Re: Proba
D'accord merci.
Pouvez vous m'aider pour la 3) svp
Pouvez vous m'aider pour la 3) svp
- 21 Juin 2017, 18:30
- Forum: ✯✎ Supérieur
- Sujet: Proba
- Réponses: 7
- Vues: 322
Proba
Bonjour, 1)Définir la notion de variable aléatoire Une var aléatoire X est une application mesurable de ( \Omega, P(\Omega),P) \rightarrow (\Z , P(\Z)) 2)Soit X une variable aléatoire réelle définie sur un espace probabilisé muni d'une mesure de probabilité P. Définir P_X...
- 21 Juin 2017, 18:14
- Forum: ✯✎ Supérieur
- Sujet: Proba
- Réponses: 7
- Vues: 322
Re: Topologie
Je n'arrivais pas à faire la différence entre ces 2 ensembles mais je comprends mieux maintenant, merci
- 08 Juin 2017, 00:26
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 3
- Vues: 237
Topologie
Bonsoir, Soit \ U= \R^2 \backslash \{(0,0)\} . Montrer que U est un ouvert de \R^2 . U=(\{(x,y)\in \R^2 , x>0 \} \cup \{(x,y)\in \R^2 , x<0 \}) \cap (\{(x,y)\in \R^2 , y>0 \} \cup \{(x,y)\in \R^2 , y<0 \}) . Est-ce que mon U est juste ? Et pour...
- 07 Juin 2017, 20:08
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 3
- Vues: 237
Re: Topologie
J'ai une dernière question, si on me demande de calculer l’adhérence de A. J'en déduis que \overline{A}=\{(x,y)\in R^2 ; x\geq 0, y\geq 0 \ x+y \leq 1 \} . Je sais que pour le prouver , il faudra montrer que tous les points sont dans \overline{A} et que c'est un ensemble fermé. C'est fermé p...
- 06 Juin 2017, 18:05
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 11
- Vues: 649
Re: Topologie
Ah ok , je peux dire que (0,-1/n)  mais pas (0,0) donc non fermé.
mais pas (0,0) donc non fermé.
- 06 Juin 2017, 17:43
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 11
- Vues: 649
Re: Topologie
D'après le cours on sait que si 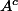 non fermé alors
non fermé alors  non ouvert. Comment montrer que
non ouvert. Comment montrer que
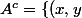\in \mathbb{R}^2\ ;\ x< 0\ {\rm ou}\ y< 0\ {\rm ou}\ x+y \ge 1 \}) n'est pas fermé avec les suites ? Je n'en trouve aucune
n'est pas fermé avec les suites ? Je n'en trouve aucune
- 06 Juin 2017, 00:18
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 11
- Vues: 649
Re: Topologie
J'ai une autre question, pour le complémentaire de A, on change juste x+y<1 en x+y  1 c'est bien ça ?
1 c'est bien ça ?
- 05 Juin 2017, 20:49
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 11
- Vues: 649
Re: Topologie
Merci pour la démo
- 05 Juin 2017, 20:44
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 11
- Vues: 649
Re: Topologie
http://www.bibmath.net/ressources/index.php?action=affiche&quoi=mathspe/methodes/topoevn.html J'ai utilisé la méthode qu'il y a sur ce site dans la sous partie " démontrer qu'un ensemble n'est pas ouvert"
- 05 Juin 2017, 20:37
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 11
- Vues: 649
Topologie
Bonsoir, On considère cette partie de R^2 muni d'une norme usuelle: A= \left\{ (x,y) \in R^2 , x\geq 0 , y \geq 0 , x+y < 1 \right\} A est-elle ouverte ,fermée, compacte , bornée dans R^2 ? Non fermée car (1-1/n,0) \in A mais pas sa limite (1,0) Non ouverte car (0,0) \in A mais pas (1/n,1/n)...
- 05 Juin 2017, 20:17
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 11
- Vues: 649
Re: Topologie
Merci pour votre aide
- 04 Mai 2016, 20:00
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 8
- Vues: 396
Re: Suite gémotrique
Salut ,
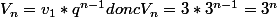

- 04 Mai 2016, 18:24
- Forum: ✯✎ Supérieur
- Sujet: Suite gémotrique
- Réponses: 5
- Vues: 351
Re: Topologie
Je pense avoir trouvé: F = {(x, y, z) / x² + y² + z² < 4} <=> F = \left\{ (x, y, z) / \sqrt{(x-0)^2 + (y-0)^2 + (z-0)^2}< 2 \right\} Donc F = B_{||.||_2}( \vec{0},2) . Donc F est ouvert. E^c= \left\{ (x,y,z) / x^2+y^2+z^2 \leq 1 \right\} <=> E^c= \left...
- 04 Mai 2016, 17:40
- Forum: ✯✎ Supérieur
- Sujet: Topologie
- Réponses: 8
- Vues: 396
- 50 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
