Forum de Mathématiques: Maths-Forum

Salut. J'ai un petit exo d'analyse que je ne trouve pas la solution. J'ai essayé l'absurde pour utiliser l'inégalité des pentes mais sans résultat Voila l'énoncé : g de classe C2 sur [a,b] g(x) >= 0 g''(x) <= 0 il existe c dans ]a,b[ tq g(c)=0 Mq g=0 sur [a,b] Vos idees sont les bienvenues. Et merci...

Merci pr la réponse

Salut, J'ai croisé cette propriété, qui dit que tout fonction définie sur R, continue, telle que \lim\limits_{x \to \infty} f(x+1) - f(x) = 0 vérifie \\lim\limits_{x \to \infty} f(x)/x = 0 Pour trouver le resultat général pour limite = l il suffit de poser g(x) = f(x) -lx Mai...

Une première remarque : vu que 0<k<1 tu aurait intérêt à écrire plutôt des 1-k et 1-k^n (qui sont positifs) plutôt que leurs opposés : ça risque de t'éviter de faire des conneries (par exemple multiplier une inégalité par un négatif...) Sinon, j'ai l'impression que ton résultat est bon, mais tu n'e...

Hello, Montre déjà par récurrence que : |x_{n+1} - x_n| \le k^n|x_1-x_0| et après tu peux sommer pour n allant de 0 à m La relation est facile à vérifier, après la somme j'ai obtenu en utilisant l'inégalité triangulaire : |x_{m+1} -x_0| \le |x_1-x_0| \frac{k^{m+1} -1}{k-1} Est ce que c'est le bon c...

Ah je vois, l'énoncé original dit que si on a
avec
Alors converge.
J'ai arrivé à montrer que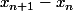 tend vers 0. Mais là je bloque.
Si vous avez des pistes veuillez me les passer.

Salut,
Si la limite
Est ce qu'on peut dire que Un converge?
Et merci d'avance

Est qu'il y a une relation pour l'indicatrice de l'union d'une famille d'ensemble.
On sait que
Que peut-on dire de :
?

jlb a écrit:pourquoi pas pour le dénominateur mais pour le numérateur?????
[ c'est au dénominateur]

Oui tout à fait, j'ai juste pas fait gaffe

C'est vrai j'ai pas respecté l'indice j'ai fait mon calcul de k=1 je pense. Idem pour la limite je l'ai calculer en utilisant la propriété lim en 0 sinx/x = 1 et là aussi il y a un problème en fait la limite est 0.

Sinon vous avez une idée comment calculer la primitive ?

Merci pour la réponse,
Voila le terme general donc



et la limite est donc 2

Oui c'est indétérminé(ça change), d'ailleurs je suis un peu surpris, vous êtes sur que l'intégrale n'est pas nulle ?

Bonjour, Je viens de passer un concours de l'ensa (école d'ingenieurs) et j'ai trouvé cet exercice qui demande de calculer la limite d'une suite défini par u_n = \prod_{k=0}^n cos(\frac{2^k \pi }{2^n -1}) J'ai essayé l'encadrement de Un pour en prenant 0<k<n mais ça ne donne rien, juste par ...

Salut, Savez vous une méthode simple pour calculer cette intégrale ? \int_0^{\pi} \frac{\sqrt{sin(x)}}{\sqrt{sin(x)}+\sqrt{cos(x)}} dx Si on change de variable t = sinx ou t=sqrt(sinx) on s'apperçoit que l'intégrale s'annule mais je veux savoir s'il y a moyen de la calculer c...

Oui je vais essayer

M.Floquet a écrit:Si tu n'aimes pas la chimie pourquoi aller en PCSI ?

Car la fillière MPSI ne m'a pas accépté

Salut, Je viens d'avoir mon bac, et j'ai reçu les réponses des classes préparatoires scientifiques en France, or je n'ai eu d'acceptation que dans la fillière PCSI, ce qui est contre mes ambitions et mes désirs, j'aime étudier les maths et la théorie plus que la chimie, donc je me demande si je peux...

Salut,
Comment déterminer les valeurs de a pour que l'équation admet des solutions

Salut, J'ai besoin de prouver une inégalité Comment démontrer que quelque soit n appartenant à N\{0,1,2} n!+1 < (n+1)^n ? Si vous avez des juste comment démontrer que n!+1 est différent de (n+1)^n c'est bon. (J'ai pensé à définir la suite Un = n!+1 - (n+1)^n et démontrer sa décroissance mais en vain)