Forum de Mathématiques: Maths-Forum

Zebulon a écrit:J'ai corrigé mon précédent message qui donne x et y en fonction de z.

Je vais regarder tout ca. la je vais me coucher car demain le travail. Je te remercie d'avoir passer autant de temps a m'aider. merci beaucoup

En fait, non. Ce n'est pas exactement ça. C'est \Large z={(x+y+1)(x+y+2)\over2}+x . non c'est bien la formule de yos. la formule: \Large z={(x+y+1)(x+y+2)\over2}+x donne X Y z 0 0 1 0 1 3 1 0 4 0 2 6 1 1 7 2 0 8 0 3 10 1 2 11 2 1 12 3 0 13 0 4 15 1 3 16 2 2 17 3 1 18...

Il semblerait que \Large z={(x+y)(x+y+1)\over2}+x , non ? C'est la fonction que proposait Yos. oui c'est ca. Je cherche une fonction pour retrouver x et une fonction pour retrouver y. Je voie qu'il y a quelque chose: x y z 0 0 0 0 1 1 1 0 2 la somme x+y fait 1 on decremente y a part...

Zebulon a écrit:C'est dans quel contexte au fait ?

C'est pour faire du codage en informatique

X Y z --- X Y z 0 0 0 --- 4 3 32 0 1 1 --- 5 2 33 1 0 2 --- 6 1 34 0 2 3 --- 7 0 35 1 1 4 --- 1 7 37 2 0 5 --- 2 6 38 0 3 6 --- 3 5 39 1 2 7 --- 4 4 40 2 1 8 --- 5 3 41 3 0 9 --- 6 2 42 0 4 10 --- 7 1 43 1 3 11 --- 2 7 47 2 2 12 --- 3 6 48 3 1 13 --- 4 5 49 4 0 14 --- 5 4 50 0 5 15 --- 6 3 51 1 4 16...

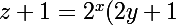Zebulon a écrit:Mon y, je ne le sors pas d'un chapeau, je résouds seulement avec x et z connus.
De rien ! :we:

J'avais compris. Seulement on trouve x sans connaitre y. Je voulais pouvoir trouver y sans connaitre x.
Encore merci

Je te remercie

\displaystyle{(a,b)\mapsto\frac{1}{2}(a+b)(a+b+1)+b} doit être bijective. Comment retrouve t on x et y ? x y z 0 0 0 0 1 1 1 0 2 0 2 3 1 1 4 2 0 5 0 3 6 1 2 7 2 1 8 3 0 9 0 4 10 1 3 11 2 2 12 3 1 13 4 0 14 1 4 16 2 3 17 3 2 18 4 1 19 2 4 23 3 3 24 4 2 25 3 4 31 4 3 32 4 4 40

Bonsoir, dans la même idée que l'autre exercice, on peut poser \Large f(x,y,z)=2^x3^y5^z . Alors pour tout entier naturel w, il existe un unique entier naturel x, un unique entier naturel y et un unique entier naturel z tels que f(x,y,z)=w. Comment fait on pour retrouver x,y,z a partir de w...

Parfait ! \Large z=2^x(2y+1)-1\ \Longleftrightarrow\ z+1=2^x(2y+1) 2^x est la "partie paire" de z+1 et 2y+1 est la "partie impaire" de z+1, on en déduit x et y. Par exemple, si z=119, alors z+1=120=2^3.15 où 3 est la plus haute puissance de 2 divisant 120 donc x=...

Zebulon a écrit:Bonsoir,
x, y et z sont-ils des entiers et x entier naturel ?

oui .

Bonjour,

Je voudrais a partir de 3 entiers n'en faire plus qu'un et pouvoir les retrouver ensuite.
Par exemple si l'on a x, y et z on obtient w.
Comment faire pour retrouver x, y et z a partir de w ?
Ceci porte il un nom ?

Cordialement

Bonjour,

A partir de 2 nombres x et y on obtient z.
Le but est de retrouver x et y a partir de z sachant que:

z=2^x(2y+1)-1

Comment dois je faire pour résoudre cette equation ?

Cordialement