Forum de Mathématiques: Maths-Forum

Bonjour a vous tous , j'ai un petit problème sur un principe de récurrence pour les suites numériques . J'ai nommé la propriété P n = 0 <U n < 1 (U n ) est une suite définie sur \mathbb{N} par : U 0 = a et 0 < a < 1 De plus , pour tout entier n , U n+1 =U n (2-U n ) Je veux montrer Que P n est vraie...

désolé bonjour évidemment mais dans la précipitation j'ai oublié l'élementaire :marteau:

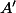est le milieu du segment [BC] , je l'ai marqué dans l'énoncé

enoncé : Soit ABC un triangle et A' , B' , C' milieux respectifs de [BC] , [CA] , [AB] . h est le complexe défini par h=a+b+c ou a , b , c sont les affixes respectifs des points A , B et C . h est affixe de H . O est le centre du cercle circonscrit au triangle ABC j'ai démontré dans la q...

ouai mais je vois pas a quoi sa va servir au fait ils me mettent une piste qui dit justement de trouver que (h-a)/(c-b) est un imaginaire pur .
J'ai cherché mais je ne trouve pas a quoi ça sert
j'ai un peu d emal avec les complexes :mur:

On me donne un triangle et son cercle circonscrit , h=a +b +c ou a , b ,c sont les affixes des points A B C et A' B' C' milieux respectifs de [BC] , [CA ]et [AB] . On peut utiliser un repère d'origine O , qui est le centre du cercle circonscrit il faut démontrer que H est orthocentre du triangle ABC...