27 résultats trouvés
Revenir à la recherche avancée
Bon, eh bien mon professeur nous a donné le corrigé du DM. Finalement il fallait bien laisser la réponse que j'ai trouvé : \prod_{k=1}^{n}(Z^k+\overline Z^k)=\prod_{k=1}^{n}\rho^k (e^{ik\theta}+e^{-ik\theta})=2^n\rho^{\frac{n(n+1)}{2}}\prod_{k=1}^{n}cos(k\theta) Elle ...
- 09 Jan 2014, 15:35
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
J'ai rendu mon DM, j'ai donc simplement laisser cette réponse : 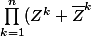=\prod_{k=1}^{n}\rho^k (e^{ik\theta}+e^{-ik\theta})=2^n\rho^{\frac{n(n+1)}{2}}\prod_{k=1}^{n}cos(k\theta))
Je vous dirais quand j'ai la correction.
Je vous dirais quand j'ai la correction.
- 06 Jan 2014, 19:28
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Comment est-ce que tu trouve cela ? J'ai essayer avec n=2 et \theta=3 J'utilise : cos(\theta)cos(n\theta)=2cos(\frac{n+1}{2}\theta) cos(\frac{n-1}{2}\theta) D'une part : cos(3)cos(2\times 3)\simeq -0.95 D'autre part : 2cos(\frac{2+1}{2}\times 3)...
- 04 Jan 2014, 23:59
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
- 04 Jan 2014, 17:47
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Notre professeur ne nous a donner aucune indication, c'est un exercice d'un DM que je dois rendre Lundi. Si d'ici là je ne trouve pas la solution ce n'est pas bien grave mais je vous tiendrais au courant dès que j'aurais la correction.
- 04 Jan 2014, 16:38
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
OK, je vois mon erreur mais je ne désarme pas. Tu parais manier sans problème les arcanes de TEX. J'ai compris quelques petites choses en prenant un de tes messages et en regardant le code-source mais peut-être pourrais-tu me donner une indication sur un tutoriel qui existerait quelque part. D'avan...
- 04 Jan 2014, 13:33
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Bon, enfaîte je viens de comprendre qu'il faut exprimer tout ça en fonction de  et
et  uniquement et pas de
uniquement et pas de  donc ça laisse entendre que
donc ça laisse entendre que 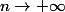 on devrait donc chercher cela :
on devrait donc chercher cela :
) avec
avec 
- 03 Jan 2014, 21:20
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
J'ai l'impression qu'on ne peut pas trouver de formule explicite. Car si on revient au résultat que j'avais trouvé (et que géotype a corrigé): \prod_{k=1}^{n}(Z^k+\overline Z^k)=2^n\rho^{\frac{n(n+1)}{2}}\prod_{k=1}^{n}cos(k\theta) On prend \theta=\frac{\pi}{8} . Et bien pour...
- 03 Jan 2014, 20:48
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Merci pour ton aide Frede, j'avais aussi vu que lorsqu'on développait pour n=1 ou n=2 on avait bien la somme d'une suite géométrique n=1 : (E^2+1) n=2 : (E^6+E^4+E^2+1) Mais lorsqu'on passe à n=3 : (E^{12}+E^{10}+E^8+2E^6+E^4+E^2+1) Et ce 2E^6 nous gène De même : n=4 : (E...
- 03 Jan 2014, 20:21
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Qu'est-ce que j'ai dis de mal ? Je ne fais absolument aucune critique, c'est pas la peine de réagir comme ça.
- 03 Jan 2014, 19:25
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Je suis en 1er année prépa MPSI et je n'ai pas encore vu les coefficients de Tchebychev. Je pense que la solution est bien plus simple. D'ailleurs le résultat ne doit pas comporté de somme ( ) ni de produit (
) ni de produit (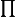 ) mais seulement des fonctions de
) mais seulement des fonctions de  et
et 
- 03 Jan 2014, 18:06
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
- 03 Jan 2014, 15:25
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
J'ai toujours rien trouvé... Si quelqu'un peut me donner un petit coup de pouce ce serais bien sympa
- 03 Jan 2014, 12:43
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
J'ai toujours rien trouvé... Si quelqu'un peut me donner un petit coup de pouce ce serais bien sympa
- 02 Jan 2014, 18:30
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Bon et bien je ne trouve toujours pas... Quelqu'un peut m'aider avec ce problème ? J'ai beau essayer tout ce que je connais mais rien n'y fait, je ne trouve pas la solution :(
- 01 Jan 2014, 18:44
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Donc avec ta méthode je trouve : \rho^n \times \frac{\prod_{k=1}^n e^{i2k\theta}+1}{e^{i\theta\frac{n(n+1)}{2}} Soit avec ta notation : \rho^n \times \frac{(E^2+1)\times (E^4+1)\times ... \times (E^{2n}+1)}{E^{\frac{n(n+1)}{2}} Effectivement le produit du déno...
- 01 Jan 2014, 16:06
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Produit de complexe
Bonjour, Pour faire cours, voici l'énoncé : Calculer \prod_{k=1}^{n}(Z^k+\overline Z^k) (en fonction de \rho et \theta ) avec Z=\rho e^{i\theta} Donc calculer : (Z+\overline Z)(Z^2+\overline Z^2)...(Z^n+\overline Z^n) Mon avancement : \prod_{k=1}^{n}(Z^k+\overline...
- 30 Déc 2013, 18:08
- Forum: ✯✎ Supérieur
- Sujet: Produit de complexe
- Réponses: 46
- Vues: 2194
Démonstration qui réutilise ce qu'on veut démontrer...
Bonjour, j'ai effectuer en classe une démonstration mais comme vous avez pu le lire dans le titre, on réutilise ce qu'on veut démontrer dans la démonstration. Alors voici l'énoncé ainsi que la démo et dites moi ce que vous en pensez : Énoncé : Montrer que \forall x \in {\mathbb {R}}, \forall n \in {...
- 11 Nov 2013, 18:39
- Forum: ✯✎ Supérieur
- Sujet: Démonstration qui réutilise ce qu'on veut démontrer...
- Réponses: 5
- Vues: 1437
Pour la toute 1ère question déjà tu dit que \lim_{n\to +\infty} u_n = L , puis tu sais que la limite de la somme de 2 suites c'est l'addition de chacune de leur limite. Tu sais aussi que u_{2n} est une suite extraite de u_n donc elle converge vers L, au final tu dois résoudre L + \frac L 2 = 1 \Left...
- 10 Nov 2013, 18:55
- Forum: ✯✎ Supérieur
- Sujet: Aidez moi svp !
- Réponses: 12
- Vues: 649
- 30 Oct 2013, 19:09
- Forum: ✯✎ Supérieur
- Sujet: Exercices nombre complexe
- Réponses: 7
- Vues: 403
- 27 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
