Forum de Mathématiques: Maths-Forum

Carpate a écrit:Oui, c'est ça

Oh génial ! Après vérification .... ça marche !
Merci beaucoup de ton aide, et celui des autres aussi mais bon voilà ... C'est cool ! Merci

Carpate a écrit:Donc tu as trouvé la solution ?

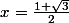
Oui, j'ai trouvé deux solutions, soient :

* (1 + 3)/2
* (1 - 3)/2

Mais seule la première solution ((1 + 3)/2) est possible car elle est positive, est-ce ça ?

hbachh a écrit:je crois que oui et ne lit meme pas le message d'avant, j'ai fait une faute sur la derniere solution :marteau:

D'accord, pas de problème ! Merci quand même

Si tu poses cette question c'est que tu n'as pas lu ce que je t'ai déjà écrit : T u as le choix entre 2 méthodes : 1) celle que tu utilises c'est-à-dire élever au carré sans précaution mais tu introduis une solution parasite, donc il te faudra contrôler si les racines obtenues conviennent c'est-à-d...

Shew a écrit:Non puisque le delta est faux dans votre post principal , il faut donc recalculer les racines en fonction du bon Delta .

Ah oui, j'avais pas recalculé après avec delta vaut 12 ...

Donc maintenant, je trouve :

x1 = (1+ 3)/2

x2 = (1- 3)/2

C'est ça ?

Ouais bon, on laisse le "OU ALORS" de coté ! ;)

Les deux racines que j'ai trouvé sont bonnes alors ?

Shew a écrit:Le delta est faux il vaut 12 .

Oui je viens de m'apercevoir, merci =)

Pour la partie "OU ALORS" comment peux-tu justifier le passage de -x² + 2x +1 = x² à 2x+1 = 0 ? La première version est la bonne. Tu as le choix entre 2 méthodes : 1) celle que tu utilises c'est-à-dire élever au carré sans précaution mais tu introduis une solution parasite, donc il te fau...

Bonjour, je suis coincé sur une équation .... Quelqu'un pourrait-il m'aider ... :$ Voici l’énoncé : Résoudre dans R l'équation ;)(-x² + 2x +1) = x Pour l'instant voilà ce que j'ai fait, surtout corrigez moi quand il la faut, je ne suis pas sur que mes pistes sont bonnes ... :/ ;)(-x² + 2x +1) = x -x...

Ah ouais d'accord !! Bah c'est bon j'ai bien compris alors ! Merci beaucoup de votre aide :)

Ah ouiii ! J'ai compris ! Les quatre solutions seront alors :
* ;)3
* ;)13
* -;)3
* -;)13

Si j'ai bien compris ? :)

ampholyte a écrit:Comme tu poses X = x² il te suffit de remplacer tous les x² par X donc

x;) - 16x² + 39 = 0
(x²)² - 16x² + 39 = 0

Je remplace X par x² donc
(X)² - 16X + 39 = 0
X² - 16X + 39 = 0

Est-ce plus clair ?

Oui c'est plus clair, je trouve donc deux solutions soient x1 = 3 et x2 = 13 c'est bien ça ?

ampholyte a écrit:Bonjour,

x;) - 16x² + 39 = 0

On pose X = x² on a donc :
X² - 16X + 39 = 0 (normalement tu sais résoudre cette équation).

Développe s'il te plaît, je ne vois pas comment tu arrives à là, après oui, je sais résoudre :$

Alors voilà, je dois résoudre une équation, mais depuis plus d'une semaine je suis dessus et pas moyen de la résoudre ... aidez moi s'il vous plaît ... :mur:

En posant X=x²

x^4-16x²+39=0

Expliquez vos démarches afin que je comprenne ! :)
Merci à bientôt ! :)