Forum de Mathématiques: Maths-Forum

En raisonnant sur la troisième égalité tu obtient facilement : a_j ln(x_j) = a_i ln(x_i) Donc si il existe 0 0 et a_i > 0 . Donc tous les x_i sont compris entre 0 et 1 Donc a_i x_i < a_1 Donc en sommant on obtient 1 < 1 d'après les deux premières données, ce qui est impossible, donc ...

L'idée de la simplification est de séparer le problème : tu veux faire la somme S = (a + kr) + (a + (k+1)r) + ... + (a + (k+p)r) pour simplifier, on "réarrange" notre somme : on met les "a" d'un coté et les termes en "r" de l'autre : S = (a + a + a + .... + a) + (kr + (k+1)r + .... + (k+p)r) Ensuite...

Tu veux calculer S = \sum_{n=k}^{k+p} a + nr Déja, tu peux arranger un peu ta somme pour la rendre plus facile a calculer : S = \sum_{n=k}^{k+p} a + \sum_{n=k}^{k+p} nr = a \sum_{n=k}^{k+p} 1 + r\sum_{n=k}^{k+p} n Du coup tu es ramené a deux somme : la première p+1. Pour calculer la deuxième, la mei...

La tu as une fonction en escalier qui n'est pas paire , pas continue. Si c'était comme j'ai dit elle serait continue paire et elle ressemblerait a un pic centré en 0

Si on veut un nombre entier de paniers (ce qui serait le plus logique), le problème est bien insoluble. En effet, si on prend plus d'une fois le panier P3, alors on a forcemment plus de 1 mangue. De même avec le panier P2, on a forcemment plus de 3 oranges. Donc on doit le faire avec seulement le pa...

Effectivement ta fonction n'est pas paire :/ se ne serai pas plus f(t) = 1 + t sur [-1, 0] et f(t) = 1 - t sur [0, 1] ?

La démonstration me parait correct, mais l'avantage des démonstrations ou l'on explicite les bases, c'est que ces démonstrations montrent aussi comment trouver P . Ceci est utile par exemple en SI, où des diagonalisations de matrices interviennent beaucoup pour simplifier les calculs, mais où il fau...

Ta relation R est bien définie sur N, elle est simplement pas très utile, vu qu'elle ne peut etre utilisé que pour x = y = 0, c'est ce qui explique que la relation est transitive, symétrique, antisymétrique. Pour détailler un peu, on peut prendre l'exemple de symétrique : R est symétrique si et seul...

Si tu pose I_n = \int_y^\infty e^{-t}t^ndt et tu veux montrer par récurrence que I_n = n! e^{-y}\sum_{k=0}^n \frac{y^{n-k}}{(n-k)!} On a I_0 = \int_y^\infty e^{-t}dt = e^{-y} , donc la relation que l'on veut montrer est vrai au rang 0. Supposons que la relation est vrai pour un n \ in \mathb...

Salut,

Procède par récurrence : avec l'intégration par partie, tu te ramène presque immédiatement au cas précédent.

Bonsoir Soit G un sous-groupe compact de GL_n(R) Comment montrez-vous que l'ensemble E= \{^tMM, M \in G \} est compact? J'ai essayé avec la définition puis de montrer que c'est l'image d'une partie compacte par une fonction continue; mais sans résultat merci Prend f : M \mapsto ^tMM elle es...

Salut, Pour la première équation : En utilisant la définition de la tangente et en mettant au même dénominateur : tan(x) + tan(4x) = \frac{sin(x)cos(4x) + cos(x)sin(4x)}{cos(x)cos(4x)} = \frac{sin(5x)}{cos(x)cos(4x&#...

Euuuuuuuuuuuuuuuuuuh .... ? Oui moi aussi j'étais très étonné du résultat quand je l'ai trouvé et je viens de voir pourquoi il était aussi très faux :cry: (Faut dire ça aurait été très très miraculeux de trouver quelque chose linéaire en fonction de la hauteur :zen: ) C'est plutot V = \pi R H^2 - \...

Le volume d'une sphère tronqué de rayon R et de hauteur H (ici H correspond à la hauteur de liquide bleue) est 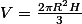donc 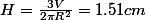d'où une hauteur de liquide rouge restante de 10,49 cm environ

Tu as oublié d'intégrer le ln(x) ce qui fait que pour le moment tu as seulement une primitive de x² + x - 3

Après une primitive de ln est xln(x) - x (tu pourras vérifier).

Du coup avec ça tu devrais trouver ce que tu cherche ;)

Pour l'exercice I : Tu pars très bien et tu as raison, il suffit de montrer que f(x) - y(x) > 0. Ta simplification de de f(x) - y(x) qui suis est également très utile. Pour te débloquer, il faut que se souvenir que un trinôme est du signe du coefficient en x² sauf entre les racines. En l'occurence ...

Le problème de ta démonstration est qu'elle est juste mais utilise la définition pour redémontrer la définition. N'oublie pas que la définition de E(a) est l'unique entier relatif vérifiant E(a) ;) a < E(a) + 1. En gros dans ta démonstration, tu utilise la définition de la partie entière sans le dir...

Dans une structure try ... catch, c'est très intuitif, comme un while qui veut dire "tant que" ou un if qui veut dire "si". Ici dans les exceptions, c'est la même chose, sauf que on dit pas "mon programme bug ou plante" mais le programme "lève une exception" ou "lancer une ecxeption". C'est pour cel...

Tu as fait une erreur en passant la 15 de l'autre coté : 5+15 = 20

tu possède la masse du papier au mètre carré, donc il faut que tu calcul la surface total des feuilles de papier, soit 200*500*(aire d'un feuille)