5 résultats trouvés
Revenir à la recherche avancée
j'ai trouvé qu'on a la convergence uniforme sur [0,1] si et ssi 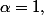 la suite
la suite  est uniformément converge sur ]0,1[
est uniformément converge sur ]0,1[
- 22 Nov 2013, 20:55
- Forum: ✯✎ Supérieur
- Sujet: Série
- Réponses: 16
- Vues: 798
Urgent
Bonjour!
Je veux étudier la convergence uniforme sur [0;1] de la suite de fonctions :
[CENTER]
 <br /> \alpha \in R.)
[/CENTER]
J'ai bloqué dans le cas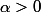 :mur:
:mur:
Je veux étudier la convergence uniforme sur [0;1] de la suite de fonctions :
[CENTER]
[/CENTER]
J'ai bloqué dans le cas
- 22 Nov 2013, 17:33
- Forum: ✯✎ Supérieur
- Sujet: Série
- Réponses: 16
- Vues: 798
- 16 Oct 2013, 17:07
- Forum: ✯✎ Supérieur
- Sujet: Série
- Réponses: 16
- Vues: 798
Monsieur23 a écrit:Aloha,
Réécris le numérateur en fonction de factorielle, puis Stirling.
merci pour l'idée :lol3:
- 16 Oct 2013, 13:59
- Forum: ✯✎ Supérieur
- Sujet: Série
- Réponses: 16
- Vues: 798
Série
Bonjour,
je veux savoir la nature de la série de terme général(n+2)...2n}{(2n)^n})
merci d'avance!
je veux savoir la nature de la série de terme général
merci d'avance!
- 16 Oct 2013, 13:26
- Forum: ✯✎ Supérieur
- Sujet: Série
- Réponses: 16
- Vues: 798
- 5 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
