Forum de Mathématiques: Maths-Forum

Sourire_banane a écrit:Quel est le premier terme de la somme partielle T_n ?

?

Sourire_banane a écrit:Ah je ne pense pas !

Raah, mais juste quand je pensais avoir fini !


Le pire dans tout ça c'est que c'est la dernière question de l'exercice et je bute dessus >< ...


Je sèche là xD

Merci à tous, en particulier à chombier pour votre aide.

J'ai pu venir à bout de l'exercice, il s'avère que la limite de Tn soit

Body... Wanna feel my boody? xDD


MMh, bref, ne nous égarons pas x)

chombier a écrit:Oui


Non

AH mince ! J'ai oublié la formule d'une série géométrique, quel idiot ... Désolé.


Pour Sn , la limite sera

Par contre, pour Tn, aurait-elle la même limite ?

chombier a écrit:On est d'accord que ?

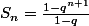
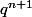
Quelle est la limite de ? Quelle est la limite de la suite ?

(en espérant ne pas me tromper) :

La limite de q^n+1 est 0 (comme nous l'avons vu car |q| < 1 ) , donc la limite de cette suite serait bel et bien 0 ?

Merci de ton aide, ça m'a vachement aidé sachant que j'étais très mal parti


Aura t-on par conséquent



et

?

Tn n'est pas la somme des n premiers termes d'une suite géométrique (comme tu l'as fait remarquer, son premier terme est q^p), il faut un tout petit peu transformer Tn pour y faire apparaitre la somme des n premiers termes d'une suite géométrique. Ok, donc cela donnerait-il Tn = http://prettyprint....

En fait tu t'es déjà trompé sur Sn (que viens faire D0 là dedans) et Tn (D0 n'a rien à y faire et ta formule est fausse, comment l'as tu construite ? Sinon, relis l'énoncé, dans tous les cas (Sn et Tn), tu as -1 < q < 1, donc (q^n) converge vers... Oui, c'est bien pour ça que j'ai corrigé (sur ma f...

Re, En effet, étourderie de ma part , je te remercie. Je remplace donc D0 par D1 dans la formule, donc pas n+1 termes mais n. Sauf que les premières questions portant sur q démarrant à 0, la formule demeure juste, faut juste pas que je confonde D0 (qui n'existe pas) et Q^0 soit W0. Donc : Si Un = 0,...

Autre question :


Les formules que j'ai mise jusqu'à présent sont-elles justes ? Car si l'on suit ce raisonnement, D0 vaudrait 0, la suite démarrerait donc à D1 ?

Re, Merci de votre aide. D0 vaudrait donc 0,7, et on aurait D1 = 0,7, D2 = 0,77 ... etc On aurait donc Un (la suite géométrique en question) = 0,7 x 0,1^n, et donc Dn = http://prettyprint.free.fr/i/41893.png ? Ou bien serait-ce une suite arithmétique ? Mais dans ce cas là je ne saurais pas vraiment ...

Salut à tous, Je viens chercher de l'aide ici car je suis un peu pommé, mais je pense néanmoins avoir bien commencé. Voici l'énoncé : Considérons la suite (dn) définie par, pour tout n appartenant à N* , Dn = 0,77......77 ------------ (n.chiffres.7) Partie A : 1) a) Pour tout n appartenant à N , et ...