4 résultats trouvés
Revenir à la recherche avancée
Re: une autre écriture de la formule : (k²+k+k'²)
Tu peux l'écrire ^2 + {k'}^2 - \frac14$) , ce qui la rendra symétrique en
, ce qui la rendra symétrique en 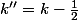 et
et 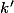 ...
...
- 13 Aoû 2017, 12:24
- Forum: ✯✎ Supérieur
- Sujet: une autre écriture de la formule : (k²+k+k'²)
- Réponses: 2
- Vues: 356
Re: ORAL ENS MATHS 2016
pour le c) Utilisons que \varphi est croissante pour l'inclusion. $\phi $ n'est pas vraiment croissante pour l'inclusion : on a par exemple $\phi( A ) = 3$ pour $A=\{ 1, 2, 3, 4\} \subset \mathbb{Z}$ (prendre $B = \{1, 2, 4\}$ , ça peut filer des idées pour la suite :frime: ), alors que $\p...
- 09 Aoû 2017, 14:06
- Forum: ✯✎ Supérieur
- Sujet: ORAL ENS MATHS 2016
- Réponses: 5
- Vues: 736
Re: ORAL ENS MATHS 2016
Pour le b), il suffit d'utiliser le lemme des tiroirs : si $A$ est réunion de $k$ sous-groupes de $G$ , alors pour toute partie $B$ de $A$ possédant $k +1$ éléments, deux d'entre eux sont dans le même sous-groupe, donc leur somme aussi. Ainsi, dans ce cas, $\phi(A)\leq k$ . Pour le c), pour ...
- 09 Aoû 2017, 13:58
- Forum: ✯✎ Supérieur
- Sujet: ORAL ENS MATHS 2016
- Réponses: 5
- Vues: 736
Factoriser, là, tout de suite, je n'ai pas d'idée (et MuPAD non plus, d'ailleurs !). Par contre, s'il s'agit de calculer l'expression en \omega=e^{2i\pi/5} , on peut faire ça : P(x)=(1+x+x^2+x^3+x^4)(1+4x^4)+5x^9 L'intérêt est que le terme 1+x+x^2+x^3+x^4 s'annule en \omega ....
- 26 Sep 2013, 23:20
- Forum: ✯✎ Supérieur
- Sujet: Simplification d'une Somme
- Réponses: 9
- Vues: 693
- 4 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
