Forum de Mathématiques: Maths-Forum

Oui clairement, en fait S est compacte je l'ai mentionné dans un des premiers messages. B inter S non vide ? Dans ce cas a priori on ne sait pas trop, on peut avoir plusieurs cas de figure... L'intersection n'est pas nécessairement connexe, en fait il est surtout intéressant de intéresser au cas où ...

Justement, que le reach soit positif c'est la bonne condition. Mais le problème est que je n'arrive pas à le montrer. Il faudrait montrer que reach >0 ==> boule tangente en tout point mais je n'y parviens pas

On remarque que la distance de l'origine à l'axe médian est 0 donc le reach est nul ! Et oui je suis bien d'accord sur ce point, néanmoins le problème est pris à l'envers : vous partez d'un point qui n'est pas sur la forme et vous montrez qu'on dispose d'une boule dont le centre est ce point et qui ...

Non, pas M_S, S. Et je suis désolé mais c'est vous qui n'avez pas compris les définitions pour le coup : je suis bien conscient qu'un tel cercle existe (celui dont vous parlez) mais ce n'est pas la définition que j'ai donnée, vous avez mal du la lire, je veux une boule qui ne contient aucun élément ...

J'imagine que S veut dire M_S plutôt, S est la forme, S son axe médian.

Je ne comprends pas trop la deuxième partie, a priori si U = lfs(x) et c est le point de l'axe médian qui minimise la distance à x, alors B(c, U) n'est pas nécessairement un bon candidat... Ou alors je n'ai pas compris.

Ah non non, le reach d'un cercle c'est son rayon. Le reach c'est le min de la lfs, comme l'axe médian d'un cercle c'est son centre seulement, la distance de tout point du cercle à l'axe médian c'est bien le rayon

Il me semble que la démonstration a une faille : si on considère un simple cercle dans R^2, qui est bien sûr à reach positif, si on prend x dessus, alors 0 adhère à l'ensemble u proposé... Donc U = 0 et la démonstration n'est pas correcte, en fait, la définition du reach n'est pas celle ci, on a pas...

Désolé pour le double-post, le me permets de reformuler ma question afin de la rendre plus orientée (sans mauvais jeu de mots). Ça va presque finir par avoir une allure d'exercice : soit S une forme à reach positif. On appelle boule tangente à S en x toute boule B(c , r) où r>0 telle que x\i...

Je connais le document de Federer bien sûr, mais il est totalement inabordable à mon niveau. La définition que je donne du reach est équivalente, pas de soucis pour ça. Voilà le document de l'X dont je parle : http://www.enseignement.polytechnique.fr/informatique/INF562/Notes/Poly_INF562.pdf Le docu...

Alors, Je ne pense pas que ceci montre l'existence d'une quelconque boule tangente à S en x si x est dans S : on parle de x quelconque sur l'axe médian avant de parler de y son plus proche voisin dans S, ça ne peut être suffisant. Il faudrait montrer l'existence d'une boule tangente à S en x pour to...

Mince je me suis mal exprimé, je voulais plutôt des exercices de maths, pas d'informatique... Enfin en tout cas, pas d'algorithmes à inventer, j'en ai déjà fait la masse pour mon TIPE
Merci quand même

Aïe aïe aïe, bête erreur d'inattention... Je reformule : on appelle plus proche voisin de à tout élément 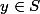vérifiant . Les autres définitions restent inchangées.
Évidemment ça change tout !

Merci déjà pour vos premières recherches

Bonjour ! Je fais un TIPE (classes préparatoires) maths-info sur la reconstruction de firmes géométriques, ça nécessite un bon bagage de topologie et de géométrie. Comme aux ENS on part vite sur des exos plutôt que sur l'exposé lui-même, auriez vous des exercices classiques à me conseiller ? Autres ...

Bonjour ! Je viens vous demander de l'aide sur un sujet qui n'est pas très classique et qui utilise des notions pas très courantes (enfin, il me semble). Ainsi il faudra s'attaquer au formalisme (pas très long heureusement) que je vais vous présenter pour vraiment comprendre la question, j'espère qu...

Toujours pas......

..................

J'ai demandé à mon prof, il a reconnu que ce n'était pas possible, il ne va donc pas essayer de rentrer des nombres de nature différente de ce qui lui est demandé :cool:

Par contre, il reste cette histoire de principe des tiroirs...

chan79 a écrit:Si tu prends deux nombres différents, tu appelles a le plus petit et b le plus grand.
On a bien alors: b-a >0 :zen:

Ah oui! Tu as raison ^^ :zen:

Et du coup, pour le faire avec le principe des tiroirs, je fais comment?.....

[quote="chan79"]Entre deux nombres réels (irrationnels ou pas), tu peux toujours trouver un rationnel. Voici une démo connue Soient deux réels distints a et b avec a0 En multipliant b-a par un entier n suffisamment grand, on a: n(b-a) >1 soit nb-na>1 il existe donc un entier p tel que na 0...

?????????????