Forum de Mathématiques: Maths-Forum

Carpate a écrit:Reprends le calcul de f(0) et de f(3) avec cette expression de f

Avec f(o) je trouve mais je vois comment continuer

J'ai fait une erreur : le x et le b font tous les deux partis de la racine : a*racine(x+b)

Bonjour ma prof m'as donné une multitude d'exercice afin de se préparer au DS de mercredi et il y a un exercice que je ne comprend pas : On considère la fonction f défini par f(x)=a*[racine de (x+b)] où a, b sont deux réels strictement positif fixés. On donne f(0)=2 et f(3)=4 Calculer les réels a et...

Pas vraiment utile d'utiliser Delta ... x²-2x+1-m= 0 puisque c'est un carré) Si m = 0 : x = 1 Si m > 0 (x-1)² <= m (x-1)² - (Vm)² <= 0 (x-1-Vm)(x-1+Vm) <= 0 x dans [1-Vm ; 1+Vm] convient. :zen: Merci beaucoup, du coup j'ai une autre question : on me demande de critiquer le résultat obtenu avec un l...

chombier a écrit:A toi de jouer pour la suite. Nombre de racines en fonction du signe de delta, etc.

Ok mais est-ce que mon delta est-il bon ?
Si ma réponse est bonne quand m>0 je ne peux pas trouver x1 et x2 car racine de -4m n'est pas un nombre positif si m>0.

chombier a écrit:c, c'est le terme constant.
m est une constante (un paramètre est toujours constant)

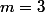
Par exemple, si , ton polynôme deviens

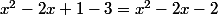
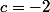
Tu retrouves , qui vérifie bien

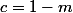
Merci pour cet éclaircissement donc du coup je trouve delta=-4m.

chombier a écrit:Bonne question.

Ton polynôme est , soit
Ainsi, a=1, b=-2, etc.

Pourquoi le 1 et le -m sont liés à c ?
Car normalement c=1, non ?

chombier a écrit:Commence par calculer le déterminant en fonction de m. Que trouves-tu ?

Merci de votre réponse mais pourquoi c=(1-m) ?

Bonjour à tous, je viens vous demander de l'aide car je ne comprend pas ce que je dois pour résoudre l'inéquation ci-après : x²-2x+1-m<=0 L'énoncé me demande de résoudre cette inéquations en distinguant les trois cas : m<0, m=0 et m>0. Dans un exercice j'ai vu qu'il fallait calculer deux fois Delta ...

titine a écrit:vec(FD) = vec(FB) + vec(BD) = -vec(BF) + vec(AB) car D est le symétrique de A par rapport à B.
= -vec(AC) + vec(AB) = vec(CA) + vec(AB) = vec(CB)

Merci car j'étais bloquer -vec(AC) + vec(AB) et je ne voyait pas comment arriver à CB.

Bonsoir à tous, j'ai une question sur un exercice que je n'arrive pas à répondre. Tout d'abord voici l'énoncé. ABC est un triangle. Le point D est le symétrique du point A par rapport au point B. E et F sont les points définis par BE=2BC+AC et BF=AC. Ma figure : http://hpics.li/da0246d La question e...