Forum de Mathématiques: Maths-Forum

godzylla a écrit:

ln, est la bijection réciproque de la fonction exp.

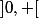
ln est dérivable sur et

est-ce que tu veux dire que la limite est 1/x. Peux-tu me donner une idée des calculs de la dérivée pour en arriver là.

merci

bonjour gou843 Merci pour le lien, mais je crois que j'ai déjà lu cette page des milliers de fois, je vous propose un autre lien bien plus intéressant, ou j'explique en détail, la répartition des nombres premiers https://sites.google.com/site/loqiquedespremiers/ Au plaisir de lire vos commentaires ...

La fonction Riemann permet le décompte des nombres premiers et si la fonction permettait d'arrêter à chaque point ou chaque zero non triviaux alors oui elle permettrait d'aligner une suite de nombres premiers. Plusieurs zéros non triviaux ont été trouvés et correspondent à des nombres premiers. Cert...

voir le lien suivant pour les formules qui génèrent des nombres premiers http://fr.wikipedia.org/wiki/Formules_pour_les_nombres_premiers bonne lecture bonjour à tous Je pense avoir trouver la répartition des nombres premiers, voici les formules que j'en ai extraits: et un exemple de leurs applicatio...

je vous soumets une variante pour le décompte des nombres premiers. le théorème sur les nombres premiers hérité de Legendre dit que le décompte est asymptotique à la fonction x/ln(x). Cette fonction reprise par Gauss deviendra somme 1/ln(x) soit une simplification à l'unité de celle de Legendre. En ...