Forum de Mathématiques: Maths-Forum

Ben314 a écrit:Effectivement : la formule générale est juste, mais je me suis (comme d'habitude...) gouré dans l'application numérique...

Bah personne n'est à l'abri de ce genre de canular... J'espère que mon v(n) fonctionne... Cevas n'a pas l'air de dire qu'il s'en est tiré...

Bien cordialement.

Ben314 a écrit:Je "voterais" plutôt pour

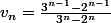
Dans votre indication plus haut, si on fait $n=1$, j'ai l'impression que l'on trouve 6=1.

Je me trompe ?

Cordialement.

Bonjour,

Posez

et calculez

Cordialement.

Jul29 a écrit:Si f'(x)>0 cela n'implique pas que f tende vers l'infini.

Je ne sais pas si un tel f existe mais il semble facile de trouver f(x)=f'(f'(x))

Bonjour,

On a en plus que f' est strictement croissante, lire le point 2) de ma réponse.

Bien cordialement.

Bonjour,

Ecrivez les indices k à partir de n+1 sous la forme k=2n-m, avec m allant de 1 à n-1, et utilisez la remarque de Doraki.

Cordialement

Bonjour, Je fais une tentative. 1) Comme f est strictement croissante, on a f^{\prime}(x)\geq 0 pour tout x , et f^{\prime}=f\circ f est strictement croissante. Si f^{\prime}(x) s'annulait pour un x_0 , elle serait strictement négative pour x0 pour tout x . 2) La fonction f(x)...

Bonjour, Voici une tentative de solution. 1) Si on fait y=x , on trouve que |f(2x)-2f(x)|\leq 2x^2 2) On montre par récurrence que |f(2^nx)-2^nf(x)|\leq (4^n-2^n) x^2 C'est vrai pour n=0 , n=1 . Si la propriété est vraie pour n , on y remplace x par 2x |f(...

Bonjour, C'est effectivement une question très intéressante, mais pas nouvelle. Voici une vieille référence: (carmichael, 1913) http://www.ams.org/journals/tran/1913-014-03/S0002-9947-1913-1500949-2/S0002-9947-1913-1500949-2.pdf En particulier (corollaire I), si on a une série entière $\sum a_n x^n$...

Bonjour,

Comme g est croissante, on a pour tout x, y:



Soit:



On remplace y par f(t), on intègre, ensuite on fait

Cordialement.