15 résultats trouvés
Revenir à la recherche avancée
Ah oui c'est bon j'ai trouvé

j'ai fait une faute de calcule :hum: vraiment stupide! Merci de m'avoir corrigé

Maintenant pour l'angle je fais:
=\frac{IM}{AI}=\frac{\sqrt{3}}{3})
Et
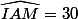
- par anonyme89
- 22 Mar 2014, 18:13
-
- Forum: ✎✎ Lycée
- Sujet: géométrie
- Réponses: 7
- Vues: 528
Alors après avoir étudié la fonction je trouve un minimum pour
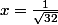
mais j'ai un doute sur la fonction dérivé c'est bien:
=\frac{2x}{\sqrt{x^2+\frac{1}{4}}}-1)
- par anonyme89
- 22 Mar 2014, 16:36
-
- Forum: ✎✎ Lycée
- Sujet: géométrie
- Réponses: 7
- Vues: 528
Tout d'abord merci de votre réponse.
Oui I est bien le milieu de [AB], j'étudie la fonction et je reviens poster ma réponse. :)
- par anonyme89
- 22 Mar 2014, 16:11
-
- Forum: ✎✎ Lycée
- Sujet: géométrie
- Réponses: 7
- Vues: 528
Bonjour, alors voilà mon professeur de maths nous a donné un exercice sur lequel on doit réfléchir mais je n'ai pas d'idée pour commencer.
- par anonyme89
- 22 Mar 2014, 15:41
-
- Forum: ✎✎ Lycée
- Sujet: géométrie
- Réponses: 7
- Vues: 528
Effectivement c'est bon, je pense que je m'etais emmêlé les pinceaux. En tout cas je vous remercie pour votre aide, et je vous souhaite une bonne fin de journée. :)
- par anonyme89
- 09 Mar 2014, 15:46
-
- Forum: ✎✎ Lycée
- Sujet: géométrie dans l'espace
- Réponses: 5
- Vues: 405
Bonjour, tout d'abord merci de votre réponse :)
J'ai essayé mais je ne tombe pas sur AH²=2, je dois faire une erreur mais le signe "-" dans la parenthèse me gène :hum:
- par anonyme89
- 09 Mar 2014, 14:08
-
- Forum: ✎✎ Lycée
- Sujet: géométrie dans l'espace
- Réponses: 5
- Vues: 405
Bonjour, alors voilà j'ai quelques petits soucis avec un exercice sur la géométrie dans l'espace, j'aimerais donc un petit coup de pouce On doit démontrer qu'une droite perpendiculaire à deux droites sécantes d'un plan est perpendiculaire à toutes les droites de ce plan. On considère deux droites sé...
- par anonyme89
- 08 Mar 2014, 21:35
-
- Forum: ✎✎ Lycée
- Sujet: géométrie dans l'espace
- Réponses: 5
- Vues: 405
Tout d'abord merci de vos réponses :we: J'ai très bien compris comment expliquer ma partie I) grâce à vos deux réponses qui m'ont beaucoup aider! Pour la partie II) je vous montre comment j'ai rédigé, j'aimerai savoir si ça convient merci Soit P(n) une propriété telle que P(0) soit vraie et telle qu...
- par anonyme89
- 07 Sep 2013, 12:35
-
- Forum: ✯✎ Supérieur
- Sujet: principe de récurrence et raisonnement par l'absurde
- Réponses: 7
- Vues: 1685
Tout d'abord merci de votre réponse.
C'est impossible que 0 soit dans A puisque A n'admet pas de plus petit élément. :we:
Hérédité: je ne vois pas trop comment montrer que n+1 n'est pas dans A :triste:
- par anonyme89
- 07 Sep 2013, 10:15
-
- Forum: ✎✎ Lycée
- Sujet: Terminale S suites et récurrence
- Réponses: 2
- Vues: 727
Bonjour, voilà j'ai un petit problème avec mon exercice de maths, j'aurais donc besoin d'aide! Mais comme personne n'a su m'aider sur le forum lycée je m'en remets à vous. :lol3: On rappelle le principe de récurrence: Théorème 1: Soit P(n) une propriété indéxée par les entiers. Si P(0) est vraie et ...
- par anonyme89
- 07 Sep 2013, 09:35
-
- Forum: ✯✎ Supérieur
- Sujet: principe de récurrence et raisonnement par l'absurde
- Réponses: 7
- Vues: 1685
Bonjour, voilà j'ai un petit problème avec mon exercice de maths, j'aurais donc besoin d'aide! On rappelle le principe de récurrence: Théorème 1: Soit P(n) une propriété indéxée par les entiers. Si P(0) est vraie et si pour tout n appartenant à N, P(n) --> P(n+1) alors P(n) est vraie pour tout n app...
- par anonyme89
- 06 Sep 2013, 17:42
-
- Forum: ✎✎ Lycée
- Sujet: Terminale S suites et récurrence
- Réponses: 2
- Vues: 727
titine a écrit:S(n+1) = 1+1/5+(1/5)²+...+(1/5)^n+(1/5)^(n+1)
Donc S(n+1) - S(n) = (1/5)^(n+1) > 0
Donc S(n+1) > S(n)
Ce qui prouve que la suite (Sn) est croissante.
Merci j'avais réussie a trouver à la fin mais par contre j'ai toujours du mal pour la dernière question qui me pose vraiment soucis :triste:
- par anonyme89
- 09 Mai 2013, 19:48
-
- Forum: ✎✎ Lycée
- Sujet: suite définie par une somme (inégalité de bernoulli)
- Réponses: 2
- Vues: 914
bonjour, alors voilà je suis élève de 1ère s et j'ai un dm de maths à faire, j'ai bien commencé mais il me manque des questions auquelles je n'arrive pas a répondre. j'aimerai un peu d'aide: j'ai démontrer dans la première partie de mon dm l'inégalité de bernoulli qui est : (1+x)^n>= 1+nx j'ai aussi...
- par anonyme89
- 09 Mai 2013, 18:13
-
- Forum: ✎✎ Lycée
- Sujet: suite définie par une somme (inégalité de bernoulli)
- Réponses: 2
- Vues: 914